Uma lâmina de água de sabão (índice de refração igual ao da água), colocado num aro vertical, escorre para baixo formando uma cunha. Observada por reflexão com luz de sódio ) incidente perpendicularmente, verifica-se que há uma franja escura no topo e 4 franjas escuras por na lâmina. Qual é o ângulo de abertura da cuna (em radianos)?
Passo 1
Vamos considerar a seguinte situação:
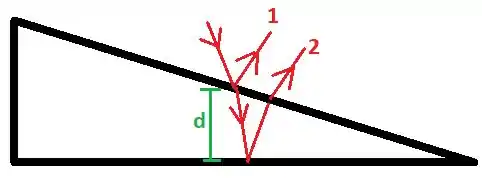
Os raios refletidos 1 e 2 vão interferir: precisamos descobrir a defasagem entre eles! A diferença de caminho entre eles é devido à espessura de sabão. Supondo incidência normal, essa diferença de caminho é o dobro da espessura da camada:
Na reflexão do raio 1 entre o ar e o sabao, como , há inversão de fase. Por outro lado, na reflexão do raio 2, não há inversão. Como há inversão de fase em uma reflexão mas não ocorre na outra, devemos somar na diferença de fase:
Assim,
Mas sabemos que
Portanto,
Mas note que dependendo da posição da cunha em que a luz incide, a espessura vai se diferente. Isso vai origem a máximos e mínimos de reflexão. Vamos focar nos mínimos, com
Assim,
Portanto,
Note que a espessura em que acontece o mínimo depende de . Portanto, vamos escrever
Passo 2
Vamos analisar o que acontece entre dois mínimos consecutivos:
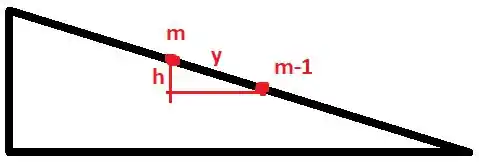
A altura é dada por
Assim,
Se temos 4 franjas a cada , a distância entre duas franjas consecutivas é
Passo 3
Com isso, temos que
Logo,
Como o seno é muito pequeno, podemos usar a aproximação:
Portanto,