Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 56

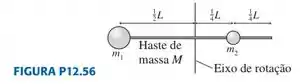
56. Determine o momento de inércia em torno do eixo do objeto mostrado na FIGURA P12.56.

Passo 1

O momento de inércia de objetos com várias partes é a soma do momento de inércia de todos eles!

O momento de inércia das duas bolinhas, por exemplo...

Primeira bolinha:

I 1 = m 1 1 2 L 2 =

m 1 L 2 4  

Segunda bolinha:

I 2 = m 2 1 4 L 2 =

m 2 L 2 16  

Para encontrar o momento de inércia da haste, no entanto, podemos fazer uma busca na tabela 12.2, percebendo que esta está bem no centro do eixo:

I h a s t e = 1 12 M L 2

Onde L é o comprimento da haste!

Passo 2

A soma dos três então...

I = I 1 + I 2 + I h a s t e   →

I = m 1 L 2 4 + m 2 L 2 16 + 1 12 M L 2   →

I = L 2 4 m 1 + m 2 4 + 1 3 M       k g ⋅ m 2

Sacou?

Resposta

I = L 2 4 m 1 + m 2 4 + 1 3 M       k g ⋅ m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o momento de inércia da área sombreada em relação ao eixo y .
Determine o momento de inércia da área sombreada em relação ao eixo x .
Determine o momento de inércia da área sombreada em relação ao eixo x .
Determine o momento de inércia da área sombreada em relação ao eixo x .
Determine o momento de inércia da área sombreada em relação ao eixo y .