Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 37

37. Uma esfera de 8,0   c m de diâmetro e 400   g de massa é liberada, a partir do repouso, do topo de uma rampa com 2,1   m de comprimento e inclinação de 25 ° . Ela rola até a base da rampa, sem deslizar.

a. Quanto vale a velocidade angular da esfera na base da rampa?

b. Que fração de sua energia cinética é energia de rotação?

Passo 1

L e t r a   A :

Vamos fazer aqui um esquema pra ver o que está acontecendo...

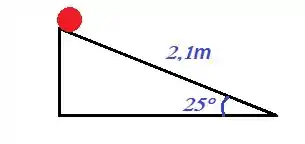
Na base da rampa, veja que toda a energia potencial do começo, vai se transformar em energia cinética, ou seja:

K = K p o t

A energia potencial pode ser calculada por...

K = M g h = M g 2,1 sin ⁡ 25

Como a Massa é 400 g = 0,4   k g , então...

K = 3,48 J

Por outro lado, podemos encontrar a energia cinética como...

K = K r o t + K c m

Onde...

K = 1 2 I c m ω 2 + 1 2 M v c m 2

Onde v c m = R ω ...

K = 1 2 I c m ω 2 + 1 2 M R 2 ω 2

Isolando ω então...

1 2 ω 2 I c m + M R 2 = K     →

ω 2 = 2 K I c m + M R 2   →

ω = 2 K I c m + M R 2

Como temos a energia, a massa e o raio, só falta determinar I c m . De acordo com a tabela 12.2, I c m da esfera é igual a 2 5 M R 2 ...

ω = 2 K 2 5 M R 2 + M R 2

Substituindo os valores...

ω = 2 ⋅ 3,48 0,4 0,04 2 2 5 + 1     →

88,13 r a d s

Passo 2

L e t r a   B :

A Energia de rotação é:

K r o t = 1 2 I c m ω 2

Logo...

K r o t = 1 2 2 5 M R 2 88,13 2     →

K r o t = 1 5 0,4 0,04 2 88,13 2     →

K r o t = 0,99   J

A fração que isso corresponde na energia total é...

0,99 3,48 = 28 %

Resposta

Letra A:

ω = 88,13   r a d / s

Letra B:

28 %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

12.32. O objeto da figura ex12.32 se encontra em equilíbrio? Explique.
33 . || Os dois objetos da F I G U R AE X 12.33 equilibram-se sobre um pivô. Quanto vale a distância d ?
Um fio fino e leve está enrolado na borda externa de um cilindro oco uniforme com massa de 4,75 kg, tendo os raios interno e externo conforme mostra a Figura abaixo. O cilindro é liberado do repouso.
9.15Q Um paradoxo: quando a haste vista na Figura 10.43 cai sem mover o pé de apoio, seu centro de massa se desloca se desloca para direita, o que significa que, devido ao atrito, a mesa exerce uma fo
9.14P Ainda com referência à haste em queda na Figura 9.20, supondo que seu ponto de apoio fique imóvel, calcule a aceleração angular em função do ângulo θ .