Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 56

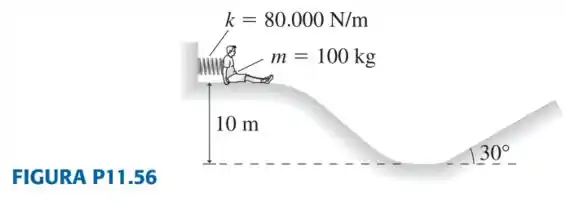
A mola mostrada na FIGURA P11.56 é comprimida em 50   c m e usada para lançar um estudante de física de 100   k g . A pista do escorregador é desprovida de atrito até ele começar a subir a rampa, e seu coeficiente de atrito cinético com a mesma é de 0,15 .

a. Quanto vale a velocidade do estudante imediatamente antes de ele perder contato com a mola?

b. Até que altura sobre a rampa subirá o estudante?

Passo 1

Quando um livro de física diz que um estudante normal de física tem 100   k g é por que talvez (só talveeeez) seja a realidade mesmo hahahah

Quando o estudante comprime a mola ele está sujeito a energia potencial elástica e gravitacional e quando ele se separa da mola ele está sujeito a energia cinética e a energia potencial gravitacional de forma que:

k Δ x 2 2 + m g h = m v 2 2 + m g h

Então:

8 × 10 4 ⋅ 50 × 10 - 2 2 2 + 100 ⋅ 9.81 ⋅ 10 = 100 v 2 2 + 100 ⋅ 9.81 ⋅ 10

Ou seja como o estudante está na mesma altura a energia potencial gravitacional não faz diferença.

Logo a velocidade do estudante será:

v = 8 × 10 4 ⋅ 50 × 10 - 2 2 100 = 14.14 m s = 10 2   m / s

Passo 2

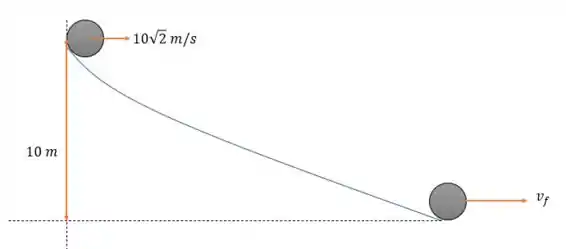
Aí beleza o estudante saiu com velocidade de 10 2   m / s mas a que velocidade ele chega no ponto mais baixo do percurso.

Bem, no começo ele tem energia cinética e potencial gravitacional, e nesse ponto mais baixo ele só tem a cinética, ou seja:

Representar o estudante como uma bola foi apenas uma coincidência hahaha

Modelando a energia nós teremos:

m g h + m v 1 2 2 = m v f 2 2

Então:

v f = 2 g h + v 1 2

Substituindo os valores nós teremos:

v f = 2 ⋅ 9.81 ⋅ 10 + 10 2 2 = 19.9   m / s

Passo 3

E aí ele começa a subir a rampa e essa rampa tem atrito então:

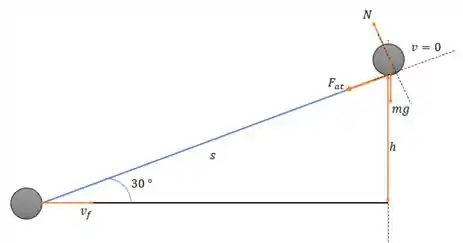
E agora a modelagem de energia é tal que somente temos a energia cinética no começo e no final temos o trabalho da força de atrito e a energia potencial gravitacional, então:

m v f 2 2 = m g h + F a t s

Onde h s = s e n   30 → h = s   s e n   30 (por propriedade trigonométrica) e F a t = μ c N = μ c m g c o s   θ então:

m v f 2 2 = m g   s   s e n   30 + μ c m g cos ⁡ 30 s

s = v f 2 2 g s e n   30 + μ c cos ⁡ 30

Pois a altura sobre a rampa é s (que é a hipotenusa desse triângulo retângulo)

Portanto substituindo os valores nós teremos:

s = 19.9 2 2 ⋅ 9.81 ( s e n   30 + 0.15 cos ⁡ 30 ) = 32.06   m

Resposta

a )   10 2   m / s

b )   s = 32.06   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

62. Prótons e nêutrons (conjuntamente chamados de núcleons) são mantidos juntos dentro do núcleo de um átomo por uma força chamada de interação forte. Para separações muito pequenas, a interação forte
49. É um belo dia com neve nova e muito lisa. Julie inicia no topo da rampa com 60 ° de inclinação mostrada na FIGURA P10.49. Na base da mesma, um arco circular a conduz para cima, descrevendo 90 ° ,
52. Você foi designado para projetar um “sistema balístico de mola” com a finalidade de medir a velocidade de balas. Uma mola de constante elástica k é suspensa ao teto. Um bloco de massa M é preso a
61. Uma partícula tem energia potencial dada por U x = x + sen ⁡ ( ( 2r a d / m ) x ) no intervalo 0m ≤ x ≤ πm . a . Onde se encontram as posições de equilíbrio neste intervalo? b . Para cada uma dela
Um foguete meteorológico de 10,2k g gera um empuxo de 200N . O foguete, apontado diretamente para cima, é posicionado sobre uma mola vertical. A base da mola, cuja constante elástica vale 500N / m , e