Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 28.Problemas - Ex. 60
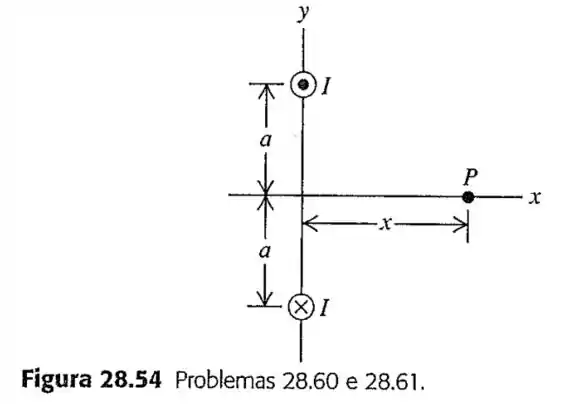
60- A Figura representa o plano que corta perpendicularmente dois fios longos e paralelos que conduzem uma corrente , de mesmo módulo, porém de sentidos contrários.
Copie o diagrama e desenhe vetores para mostrar o campo de cada fio e o campo resultante no ponto .
Deduza uma expressão para o módulo de em qualquer ponto do eixo em termos da coordenada do ponto. Qual é a direção e o sentido de ?
Faça um gráfico do módulo de em função de .
Para qual valor de o módulo de atinge seu valor máximo?
Qual é o módulo de quando ?
Passo 1
Como mostrado no exercício desse capítulo se temos um ponto inclinado em relação a corrente nós teremos um campo magnético inclinado de forma que:
O que nos dá a seguinte soma de campos magnéticos em .
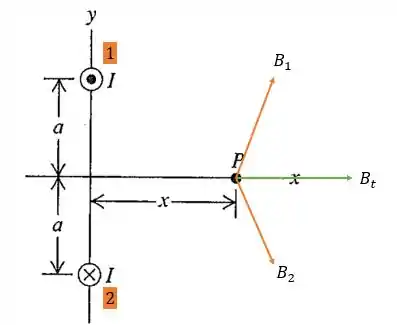
Passo 2
De forma vetorial temos o campo vetorial igual a:
Então para a corrente que sai do plano nós temos:
Onde:
O que podemos ver no diagrama do passo anterior que o vetor do campo magnético da corrente gera um vetor com componentes positivas em e em . Portanto o campo gerado pela corrente será:
Pois nesse caso:
Portanto o campo total no eixo será de:
Plotando o gráfico do campo nesse sentido teremos:
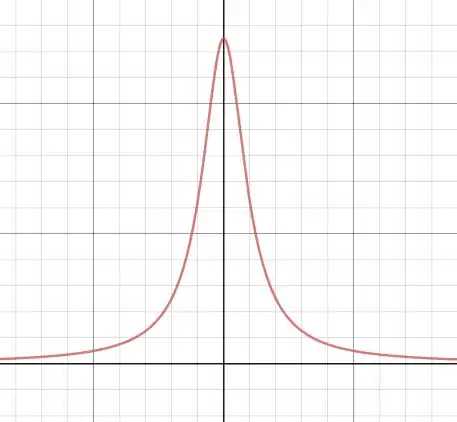
Aí a intensidade depende do valor de e da corrente, mas no geral teremos essa forma para o gráfico. Onde ele é sempre máximo com
Passo 3
Quando temos uma intensidade de campo igual a:
Pois é insignificante para , podendo ser descartada, nos dando um gráfico igual a: