Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 7.1 - Ex. 59
Um pêndulo está suspenso a partir do teto e preso a uma mola fixada no chão diretamente abaixo do suporte do pêndulo (veja a figura). A massa da bolinha do pêndulo é , o comprimento do pêndulo é , e a constante de força é . O comprimento da mola frouxa é e a distância entre o chaõ e o teto é . O pêndulo é puxado para o lado de forma a fazer um ângulo com a vertical e então é solto a partir do repouso. Obtenha uma expressão para a rapidez da bolinha do pêndulo conforme ela passa por um ponto diretamente abaixo do suporte do pêndulo.
Passo 1
Oláaaa, querido! Cê tá bem? Então, essa figura do enunciado é meio feinha né? Ela me assustou. Mas fica tranquilo, vamos começar entendendo o que está acontecendo e fazendo uma figura só nossa.
Primeiro, temos uma bolinha presa na corda de comprimento e presa na mola frouxa de comprimento . Algo assim:
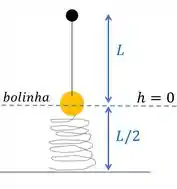
Vamos dizer que nosso referencial de altura é essa posição inicial da bolinha.
Depois alguém vai lá e puxa essa bolinha fazendo com que a corda faça um ângulo com a vertical. Isso causa um esticamento na mola, que agora vai ter uma deformação :
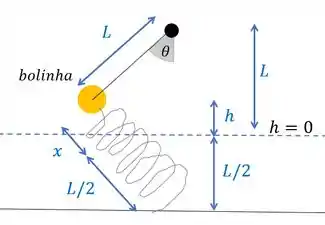
O nosso referencial não saiu do lugar, mas agora a mola e a cordinha estão inclinadas. E a mola recebe um aumento de no seu comprimento porque fica esticada.
E o que ele quer? Ele quer a rapidez da bolinha quando ela volta aquela posição inicial onde a mola está frouxa se a gente a soltar dessa última posição.
Mas como a gente acha esse ? Cara, como temos como dados as altura do elementos em alguns momentos, temos uma mola e queremos , é uma boa a gente usar a conservação de energia mecânica.
Bora começar!
Passo 2
De forma geral, a energia mecânica de um objeto é a soma da energia potencial gravitacional, a elástica e a energia cinética:
Quando você puxa o pêndulo para o lado, você dá para ele energia potencial gravitacional (porque ele ganha alguma altura) e energia potencial elástica (porque a mola é distorcida). Então a energia da bolinha nesse ponto é
A energia cinética é nula porque a bolinha está parada nesse ponto.
No segundo momento, quando a bola passa pelo ponto de equilíbrio (em que a mola está frouxa, logo , e a bolinha está na posição , e assim ), toda essa energia que ela tinha antes, terá se convertido em energia cinética porque ela ganhou velocidade:
Pela conservação de energia, como não há forças externas ao nosso sistema, a energia mecânica é igual nesses dois pontos
Substituindo as fórmulinhas de cada uma dessas energias:
Passo 3
O enunciado diz que a gente tem , e . Então para achar a expressão de a partir da expressão acima, precisamos de e .
Temos essa situação quando a corda é puxada:
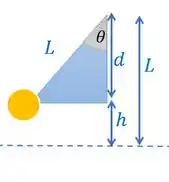
Sendo que pode ser achada por trigonometria
De modo que fica
Substituindo isso em :
Passo 4
Agora vamos procurar uma expressão para a distorção da mola. Precisamos de um desenho da situação:
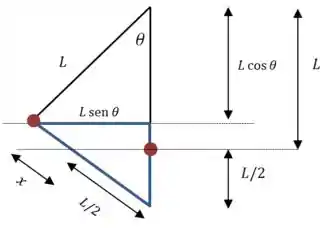
Vamos aplicar o teorema de Pitágoras sobre o triângulo azul:
Simplificando um pouco essa expressão:
Nosso objetivo aqui é encontrar , então vamos tirar a raiz quadrada dos dois lados e isolar:
Usamos só a parte positiva da raiz porque é uma distância (grandeza positiva).
Passo 5
Voltando à expressão que encontramos no passo :
Vamos isolar a rapidez que queremos calcular:
E substituindo a expressão para :
Vamos colocar em evidência:
E agora tirando a raiz quadrada dos dois lados:
Resposta
A rapidez da bolinha nesse ponto é .