Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 7.1 - Ex. 41
41. Uma criança de , em um balanço de de comprimento, move-se com uma rapidez de quando o assento de balanco passa pelo seu ponto mais baixo. Qual é o ângulo que o balanço forma com a vertical quando antinge o seu ponto mais alto? Despreze a resistência do ar e suponha que a criança não está forçando o balanço.
Passo 1
Consideremos o sistema de análise como o formado pela Terra e pela criança.Desse modo, não há forças externas atuando no nosso sistema e o trabalho das forças externas, , é igual a zero. Escolhendo, convenientemente o sistema de referencial potencial gravitacional no ponto mais baixo do balanço, como mostrado na figura abaixo, então a energia inicial da criança é inteiramente cinética. Por sua vez, quando a criança encontra-se no seu ponto mais alto, desta vez a energia é inteiramente potencial gravitacional. Com isso, podemos determinar através da conservação de energia mecânica e, em seguida, usar trigonometria para determinar . Mãos a obra!
A seguinte imagem auxilia na compreensão do que pretende-se fazer:
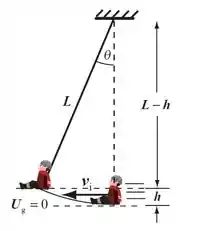
Através do uso de relações trigonométricas simples, determina-se o ângulo como sendo:
Tudo que temos que fazer agora é obter , dado o valor de .
Passo 2
Aplicando a conservação de energia mecânica para o sistema, onde é a notação de energia cinética, é a notação de energia potencial e é o trabalho da força externa, que no caso, não existe nessa situação, chegamos a:
Mas como , temos que:
Só que e , nada mais são do que a diferença entre as energias finale e inicial e ). Com isso, obtemos que:
Agora, vamos analisar com calma o nosso problema. Como descrito no , no instante inicial a criança encontra-se na altura de origem, em relação ao referencial, movendo-se com a velocidade máxima, para em seguida parar numa altura máxima . Opa! Assim, obtemos que e são na verdade, igual a De modo que obtemos a seguinte relação:
Passo 3
Agora é só substituir na relação expressa anteriormente, as fórmulas relativas a energia potencial final e a energia cinética inicial :
Mas porque calcular agora, se podemos substituí-lo de uma vez para encontrar o ângulo
que pede a questão? Vamos fazer isso:
Pronto! Resposta encontrada
Resposta
O valor do ângulo é aproximadamente igual a .