37. Um pêndulo simples de comprimento , com uma massa em sua extremidade, é deslocado lateralmente até que a massa atinja uma altura acima de sua posição de equilíbrio. A massa é então, largada. Determine a rapidez da massa quando ela passa pela posição de equilíbrio. Despreze a resistência do ar.
Passo 1
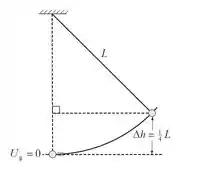
O diagrama acima mostra o pêndulo em sua posição inicial. A primeira iniciativa, quando se quer resolver esse tipo de questão, é definir um sistema de referencial. Por isso, deixamos que o ponto zero de energia potencial gravitacional esteja no ponto mais baixo de balanço do pêndulo, que na verdade é a posição de equilíbrio. Podemos encontrar a velocidade da massa na altura , simplesmente aplicando a conservação de energia mecânica para o sistema. Como já é praxe para questões de energia envolvendo pêndulos, sabemos que na altura de equílibrio, o único tipo de energia disponível é a cinética. Já quando o pêndulo atinge sua altura máxima, só há energia potencial nesse instante. O que temos que fazer é igualar as duas energias e pronto! Encontraremos a velocidade:
Passo 2
Aplicando a conservação de energia mecânica para o sistema, onde é a notação de energia cinética, é a notação de energia potencial e é o trabalho da força externa, que no caso, não existe nessa situação, chegamos a:
Mas como , temos que:
Só que e , nada mais são do que a diferença entre as energias finale e inicial e ). Com isso, obtemos que:
Agora, vamos as análises. Como descrito no enunciado, na posição inicial a massa encontra-se na altura em relação ao referencial, onde a velocidade é nula. Mas em compensação, assim que a massa chega à origem do nosso referencial, sua velocidade é máxima. Opa! Assim, obtemos que e são, na verdade, igual a e a partir daí obtemos a seguinte relação:
Passo 3
Agora é só substituir na relação expressa anteriormente, as fórmulas relativas a energia potencial inicial e a energia cinética final :
Mas o que é esse ? Bem, o nada mais é do que altura inicial em que a massa encontrava-se, que já é fornecida pelo exercício e igual a . Finalmente, podemos terminar as contas:
Resposta
A rapidez da massa na posição de equilíbrio é igual a