Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 26.Problemas - Ex. 64
64- Calcule a corrente que passa em cada resistor e na bateria do circuito indicado na Figura
Qual é a resistência equivalente do circuito?
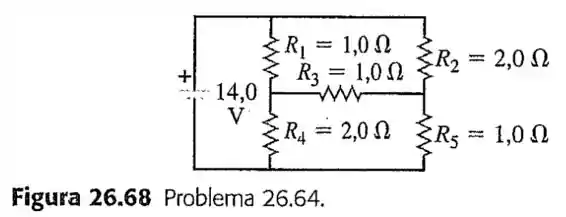
Passo 1
Vamos considerar três correntes nas três malhas do circuito tal como pode ser visto no circuito abaixo.
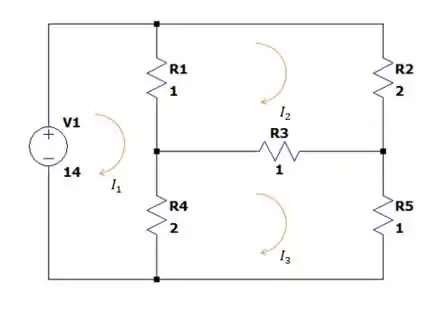
Analisando as tensões na malha nós teremos:
A somatória das tensões na malha nos dará:
E a somatória de tensão na malha :
E como não vou ensinar marmanjo velho a fazer sistema aqui vai as respostas se fizermos um sistema com as três equações:
Passo 2
Agora a corrente que passa em cada resistor:
Sem contar que a corrente que sai da bateria é de , nos dando a possibilidade de calcular a resistência equivalente desse circuito sem precisar fazer transformação triangulo para estrela, como? Basta fazer:
Resposta
Correntes na tabela do passo 2