68- No circuito indicado na Figura , todos os resistores são classificados a uma potência máxima de . Qual é a fem máxima que a bateria pode ter, sem queimar nenhum resistor?
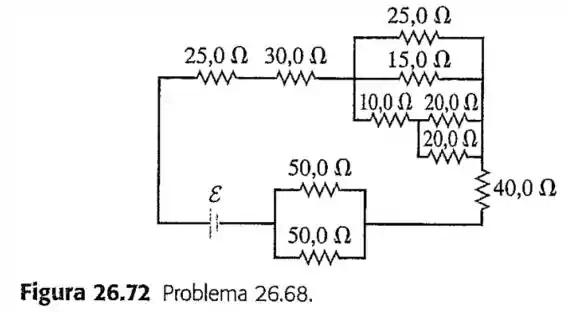
Passo 1
Vamos analisar a fórmula da potência quando temos a corrente e o resistor:
Como a potência em todos os resistores é fixa, vamos tratar ela como uma constante. Dessa forma, quanto maior a resistência menor deve ser essa corrente.
Então vamos transformar esse circuito em um circuito em série (para termos a mesma corrente) e ver qual dos seguintes resistores equivalentes será o maior.
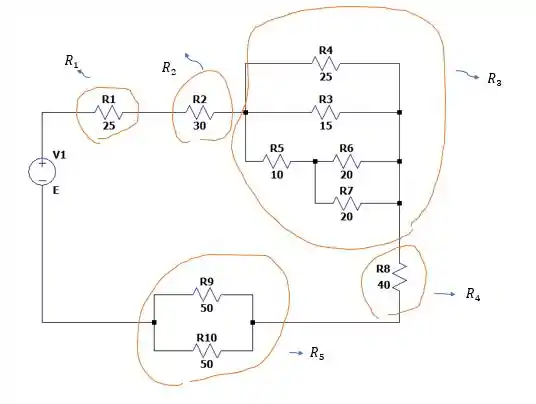
Por enquanto a resistência de é a maior de todas e é a que dita a corrente no circuito.
Porém se a resistência equivalente ou forem maiores que é provável que dentro delas passe uma corrente maior.
Fazendo nós temos:
E fazendo teremos:
O que nos dá então o seguinte circuito:
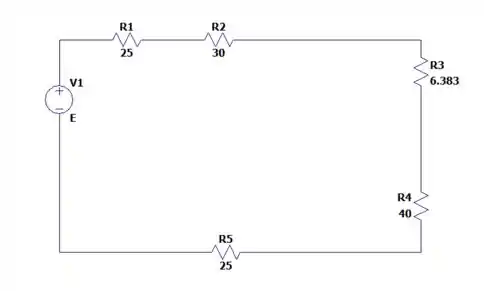
Então a corrente será limitada pela resistência de e que será de:
Se fizermos a mesma conta para todos os resistores, todos irão dar correntes maiores, o que estoura com o resistor de .
Passo 2
Então a potência total liberada pela fonte será de:
E isso nos dará uma tensão igual a: