Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 27.Problemas - Ex. 75
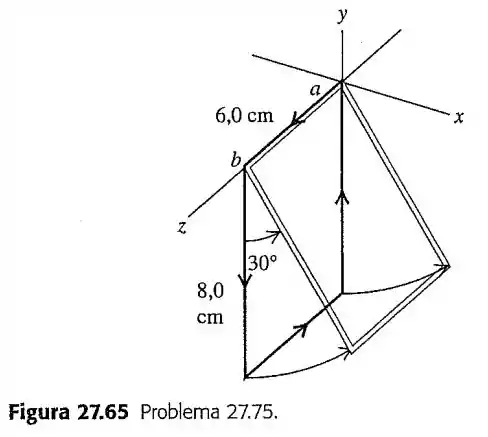
75- A espira retangular indicada na Figura possui massa igual a por centímetro de comprimento e está articulada em torno do lado por meio de um eixo sem atrito. A corrente que circula no fio é igual a , no sentido indicado. Determine o módulo, a direção e o sentido do campo magnético paralelo ao eixo que produzirá uma oscilação para cima na espira até que seu plano forme um ângulo de com o plano .
Passo 1
Bem, a questão quer o campo magnético necessário para deixar essa espira retangular estável em e dessa forma termos o seguinte diagrama de forças.
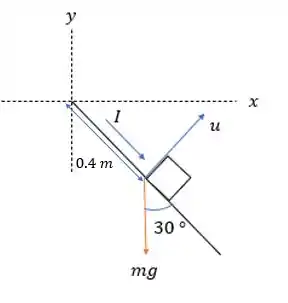
O torque gerado pela força peso no eixo será de:
E esse torque está no sentido horário do plano .
Passo 2
Como somente temos um campo magnético em na direção então, temos o outro diagrama de forças (agora elétrico).
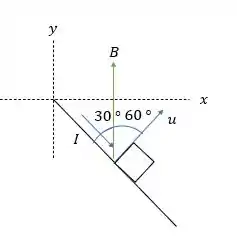
E esse campo magnético gera um torque na espira, porém ele tem que estar perpendicular a , ou seja, o campo magnético que gera torque estará em , logo o torque será de:
Torque no sentido anti-horário, opondo ao torque causado pelo peso.
Igualando os dois torques teremos: