Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 27.Problemas - Ex. 84
84-Derivação da Equação (27.26) para uma espira circular. Uma espira em fio em forma de anel está sobre o plano com o centro na origem. No anel, circula uma corrente no sentido anti-horário (Figura ). Um campo magnético uniforme . (Esse resultado poderá ser facilmente estendido para um campo com direção arbitrária.)
Na Figura , mostre que o elemento de linha é dado por e calcule .
Integre ao longo da espira para mostrar que a força resultante é igual a zero.
Do item calcule , em que é o vetor que liga o centro da espira ao elemento . (Observe que é perpendicular a )
Integre ao longo da espira para encontrar o torque total que atua sobre a espira. Mostre que o resultado pode ser escrito na forma , em que . (Nota: e ).
Passo 1
Sabendo que varia em em relação ao cosseno (pois está relacionado com a vertical) e de forma positiva (pois a posição de de cresce a medida que varia).
Já a parcela horizontal decresce a medida que cresce no sentido anti-horário e varia em relação ao seno. Então a parte vetorial de será igual a:
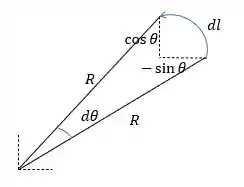
Isso nos diz que quando aponta na direção e o que aponta em é .
Então será:
Isso será:
Passo 2
Para integrar em todo o círculo nós devemos fazer com que varie em até .
Passo 3
Fazendo a conta da letra nós temos:
Fazendo produto notável (com as regras de produto vetorial) nós teremos:
Passo 4
Integrando de até em nós teremos:
Onde , então uma forma possível de escrever em termos de é:
Uma vez que o vetor está na direção . E nos diz que está na direção .