Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 27.Problemas - Ex. 82
82- Torque sobre uma espira de corrente em um campo magnético não uniforme. Na Seção , a expressão do torque sobre uma espira de corrente foi deduzida supondo que o campo magnético fosse uniforme. Porém, o que ocorre quando não é uniforme? A figura mostra uma espira quadrada que está contida no plano . A espira possui vértices nos pontos e e conduz uma corrente no sentido horário.
O campo magnético não possui componente , mas possui componentes em ambas as direções e : , em que é uma constante positiva.
Faça um desenho das linhas do campo magnético no plano .
Calcule o módulo, a direção e o sentido da força magnética exercida sobre cada um dos lados da espira, integrando a Equação .
Se a espira pode girar livremente em torno do eixo , determine o módulo, a direção e o sentido do torque magnético sobre a espira
Repita o item para o caso no qual a espira pode girar livremente em torno do eixo
A Equação , , fornece uma descrição apropriada para o torque sobre a espira? Por quê?
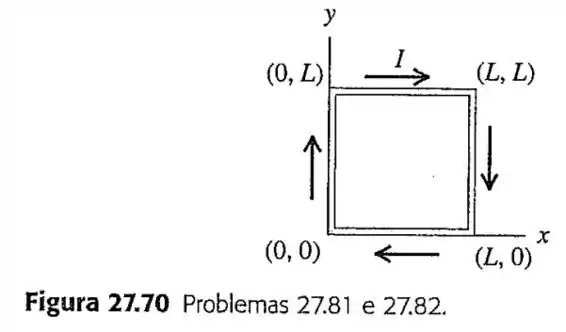
Passo 1
Utilizando o Geogebra nós temos a seguinte representação vetorial:
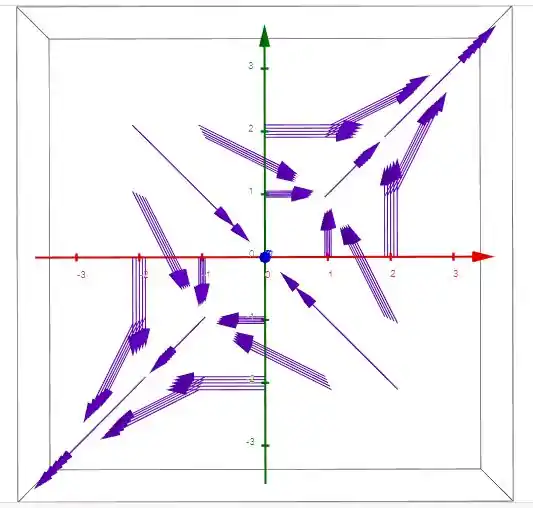
Passo 2
Agora vamos dar nome aos lados e fazer a integral da força magnética nesses lados (a integral é necessárias pois ela varia com e portanto tendo que fazer a integral em todo o seu espaço):
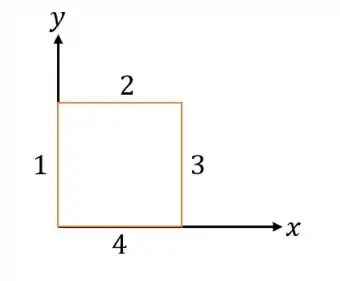
Pois vem, a força no lado será:
Agora no lado temos:
Agora para o lado :
Pois a corrente flui de cima para baixo.
Já a força no lado 4 será:
Passo 3
Sendo livre para girar no eixo então as forças nos elementos e se cancelam (a do 4 naturalmente não gera torque nenhum) então só sobra a força no elemento com um raio de giro igual a , logo:
Onde é a área da espira.
Passo 4
Já na letra temos que a espira gira em com isso temos que as forças em 2 e 4 se cancelam, gerando momento somente a força em , em um raio de giro igual a , portanto o torque será:
Passo 5
Como o campo magnético não é constante então o torque não é apropriado.