Enunciado
Física - Young and Freedman - Vol 3- Ed: 14º - Capítulo 31.Exercícios - Ex. 66
Você recebe esta tabela de dados registrados para um circuito com um resistor, um indutor com resistência desprezível e um capacitor, todos em série com uma fonte de tensão :
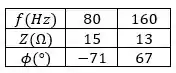
Aqui, é a frequência da fonte de tensão, é a impedância do circuito e é o ângulo de fase. Use os dados nas duas frequências para calcular a resistência do resistor. (Dica: use os resultados do Exercício 31.21.) Calcule a média desses dois valores da resistência e use os resultados como o valor de R no restante da análise. Use os dados em e para calcular a indutância e a capacitância do circuito. Qual é a frequência de ressonância para o circuito, e quais são a impedância e o ângulo de fase da frequência de ressonância?
Passo 1
Vem comigo que a gente detona com essa juntos!
Para encontrar a resistência do resistor pedido em podemos usar que:
Podemos calcular o valor de para as duas frequências e tirar um média para saber o melhor valor de .
Para o item temos que encontrar e , para isso podemos usar a seguinte equação:
Vamos usar essa equação para cada frequência e mexer nas expressões para encontrarmos e .
Para encontrar a frequência de ressonância em , podemos usar que:
Como estamos em ressonância, temos que .
Passo 2
Vamos começar com o item .
Para a frequência de , temos:
Para , temos:
Tirando uma média dessas resistências, temos:
Passo 3
Agora vamos para o item .
Vamos começar com a frequência de , temos:
Lembrando que , temos:
Agora para a frequência de , temos:
Agora vamos multiplicar a primeira equação por e somar com a segunda, assim:
Assim temos que:
Passo 4
Agora vamos jogar esse valor de em uma das equações do passo anterior e vamos encontrar .
Temos que:
Assim temos que:
Passo 5
Agora vamos para o item e encontrar a frequência de ressonância. Temos:
Agora como estamos em ressonância, temos que , a equação da impedância é dada por:
Então temos que:
E como:
Temos que .
Com isso finalizamos a questão com sucesso!