Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 7.Problemas - Ex. 70
. Um pequeno bloco com massa de desliza em um círculo vertical de raio no interior de uma pista circular. Durante uma das voltas do bloco, quando ele se encontra na parte inferior de sua trajetória, no ponto , a força normal exercida pela pista sobre o bloco tem módulo de . Nessa mesma volta, quando o bloco atinge o topo da trajetória (ponto ), a força normal exercida sobre o bloco tem módulo . Quanto trabalho é realizado pelo atrito sobre o bloco durante o movimento do bloco do ponto até
o ponto ?
Passo 1
Vem comigo que a gente se livra dessa juntos!
A trajetória que bloco segue é bem dizer essa aqui:
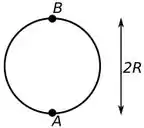
O segredo desse problema é usar a conservação de energia ao nosso favor, mas temos que nos atentar que nesse sistema temos uma força dissipativa (força de atrito) que realiza trabalho, então temos que:
Considerando o ponto como sendo o ponto onde temos o zero de energia potencial gravitacional, ficamos com:
Para calcular a energia potencial já temos tudo o que precisamos, agora para calcular e precisamos saber a velocidade do bloco nesses pontos.
Para isso vamos usar a segunda lei de Newton, lembrando que a força resultante sobre o bloco é igual a força centrípeta por conta do movimento circular.
E as únicas forças que agem sobre o carrinho na vertical é a força normal e a força peso.
Passo 2
Vamos primeiro encontrar a velocidade no ponto , usando a segunda lei de Newton, temos:
Isolando , temos:
Substituindo os valores que conhecemos, temos:
Passo 3
Agora vamos encontrar a velocidade em , temos:
Isolando , temos:
Substituindo os valores que conhecemos, temos:
Passo 4
Agora que temos as velocidades nos dois pontos, podemos calcular o trabalho pedido no enunciado. Temos:
Substituindo os valores que conhecemos, temos:
Assim temos que:
Questão finalizada com sucesso!