Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.Problemas Adicionais - Ex. 117
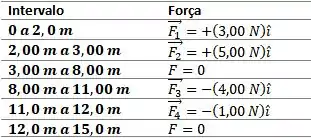
Uma partícula pode se mover apenas ao longo de um eixo , sob a ação de forças conservativas (Fig. 8-64 e tabela). A partícula é liberada em com uma energia cinética e uma energia potencial . Se a partícula se move no sentido negativo do eixo , qual é o valor (a) de e (b) de em e o valor (c) de e (d) de em ? Se a partícula se move no sentido positivo do eixo , qual é o valor (e) de e (f) de em , o valor (g) de e (h) de em e o valor (i) de e (j) de em? (k) Plote em função de para o intervalo de a .
Figura 8-64 Problema 81
A partícula é liberada a partir do repouso em . Quais são (1) a energia cinética em e (m) o valor máximo de, atingido pela partícula? (n) O que acontece com a partícula após atingir ?
Passo 1
a) Quando a partícula se move de até , o trabalho é
Como e
No início do movimento, e , logo a energia máxima do sistema
Logo, no ponto de
Passo 2
b) Como já calculada no item
Passo 3
c) O trabalho realizado quando a partícula vai de a
A energia potencial em
Logo,
Passo 4
d) Como calculado no item
Passo 5
e) Quando a partícula se move de até , o trabalho realizado é
Logo
E a energia cinética
Passo 6
f) Como calculado no item
Passo 7
g) O trabalho realizado de até
E
Logo
Passo 8
h) Como calculado no item
Passo 9
i) O trabalho realizado de até
Logo
Então
Passo 10
j) Como calculado no item
Passo 11
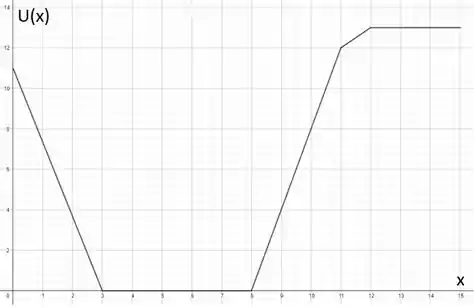
k) A partir dos dados obtidos nos itens anteriores, plotou-se o gráfico de em função de , mostrado a seguir
Passo 12
l) Toda energia potencial no início () é transformada em energia cinética, então
Passo 13
m) No seu valor , a energia cinética foi totalmente convertida em energia potencial novamente, logo, utilizado o gráfico do item
Passo 14
n) Quando a partícula para momentaneamente, ela é acelerada pra esquerda pela e ganha velocidade para subir de volta até
Resposta
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)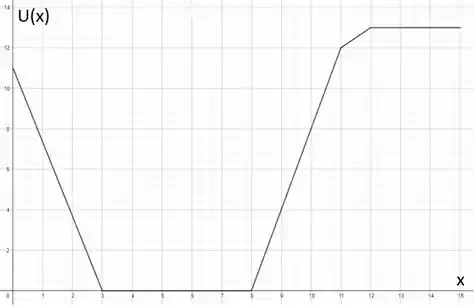
l)
m)
n) Volta até