Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 28.Problemas - Ex. 72
72- Para o cabo co-axial do Exercício , deduza uma expressão para o módulo do campo magnético para os pontos do interior do condutor central . Compare seu resultado para ao resultado obtido no item do Exercício , no mesmo ponto.
Para esse cabo co-axial, deduza uma expressão para o campo nos pontos do interior do tubo . Compare seu resultado para ao resultado obtido no item do Exercício , no mesmo ponto. Compare seu resultado para ao resultado obtido no item do Exercício , no mesmo ponto.
Passo 1
Considerando que a corrente flui uniformemente por toda a seção do fio nós teremos que a corrente que flui em um seção será de:
E pela lei de Ampere temos que na seção de será de:
E quando teremos:
O que é o mesmo valor encontrado na questão (só mudando umas variáveis ai)
Passo 2
Já na região entre temos:
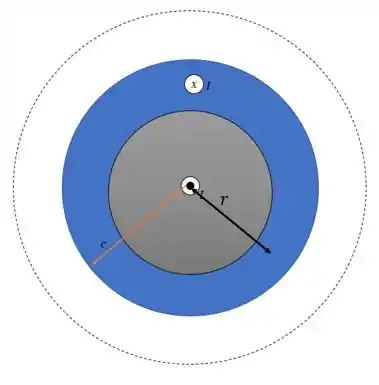
A corrente nessa região será de:
Pois quando a área azul está vazia , temos a corrente (a que está dentro de ) e quando a área está vazia a corrente é de (a soma das duas correntes).
Pois nesse caso temos que considerar a área entre regiões (pois não estamos analisando o corpo todo somente a contribuição dessa região), coisa que não precisava ser feito na questão , então pela lei de Ampere teremos.
E quando , , assim como encontrado na questão e quando assim como naquela questão e assim se manterá para .