Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 28.Problemas - Ex. 81
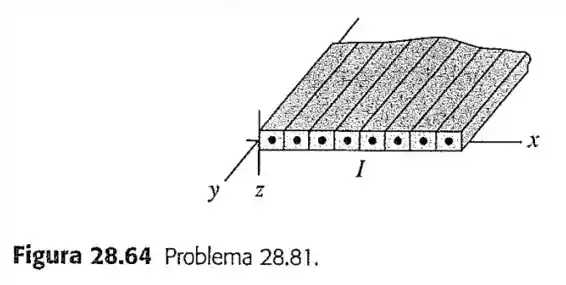
81- Um plano infinito que conduz uma corrente. Condutores retilíneos longos, com seções retas quadradas, cada um deles conduzindo uma corrente , são colocados um ao lado do outro, formando uma placa fina que se estende até o infinito (Figura ). Os condutores se distribuem sobre o plano paralelamente ao eixo e conduzem uma corrente no sentido . Existem condutores por unidade de comprimento ao longo do eixo .
Determine o módulo, a direção e o sentido do campo magnético a uma distância abaixo do plano da corrente.
Encontre o módulo, a direção e o sentido do campo magnético a uma distância acima do plano da corrente.
Passo 1
Vamos considerar dois fios quadrangulares desses e estudar o que acontece em um ponto a distância em cima e embaixo.
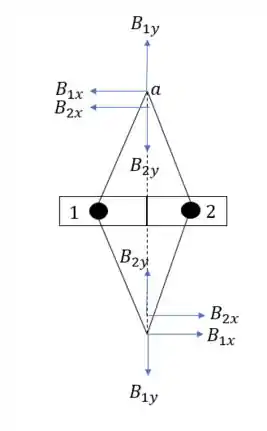
Onde pela regra da mão direita vemos que as componentes da corrente no quadrado e no quadrado no meio da conexão entre esses dois quadrados, e com ela encontramos componentes horizontais e verticais com a mesma intensidade e por terem a mesma intensidade (por serem quadrados e terem a mesma corrente) nós somente teremos componentes horizontais. Agora vamos para a fórmula desse campo.
Passo 2
Sabendo agora que temos um comprimento de painel com n condutores com direção de corrente que sai para fora do papel nós teremos os seguintes pontos a uma distância desse painel.
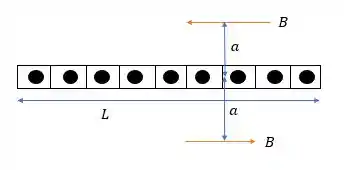
Pela Lei de Ampere temos que:
Onde a corrente total é a corrente que atravessa todo o comprimento , e como temos n condutores por uma unidade de comprimento então em uma distância temos condutores, então a corrente será:
Então:
E como o campo magnético é paralelo ao comprimento e é gerado tanto em cima quando em baixo, então a integral de superfície será de:
Então:
Campo magnético que independente de (pois é um campo totalmente horizontal) e de .