Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 27.Problemas - Ex. 72
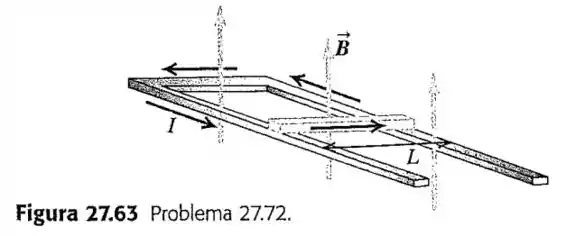
72- Propulsão elemognética em um trilho. Uma barra condutora de comprimento e massa desliza sobre trilhos horizontais conectados a um fonte de voltagem. A fonte de voltagem mantém uma corrente constante nos trilhos e na barra; e um campo magnético vertical unforme preenche o espaço entre os trilhos (Figura ).
Determine o módulo, a direção e o sentido da força resultante sobre a barra. Despreze o atrito, a resistência do ar e a resistência elétrica.
Se a barra possui massa , calcule a distância que ela deve percorrer ao longo dos trilhos, partindo do repouso , até atingir uma velocidade .
Existem teorias sobre a possibilidade de que a propulsão baseada nesse princípio possa ser usada para acelerar massas e colocá-las em órbita ao redor da Terra e,até mesmo, fazer o objeto sair da atração terrestre. Calcule a distância que a barra deve percorrer para atingir a velocidade de escape da Terra . Considere que , , e . Para simplificar, suponha que a força resultante que atua sobre o objeto é igual a força magnética, como nos itens e , embora a gravidade desempenhe um papel importante em um lançamento espacial real.
Passo 1
Pela fórmula bemos que e então a força magnética na barra terá módulo igual a:
E fazendo o desenho das componentes na barra (e ajeitando um pouco a visão também por que a vista tá um tanto isométrica) nós temos:
Então pela regra da mão esquerda vemos que a força está para a direita.
Passo 2
Por ser um movimento uniformemente acelerado( por termos uma aplicação de força constante) então podemos aplicar torricelli e por ele temos que:
Utilizar o tempo aqui poderia complicar as coisas.
Então como a barra vai partir do repouso temos que .
E como a aceleração é constante temos que
E por entemos que ele valha . Logo:
Então valerá:
Passo 3
Aplicando os valores da letra na fórmula encontrada no passo nós temos:
Uma grande distância na real.
A aceleração nesse caso será de:
O que prova que não podemos ignorar a aceleração da gravidade nesse caso.