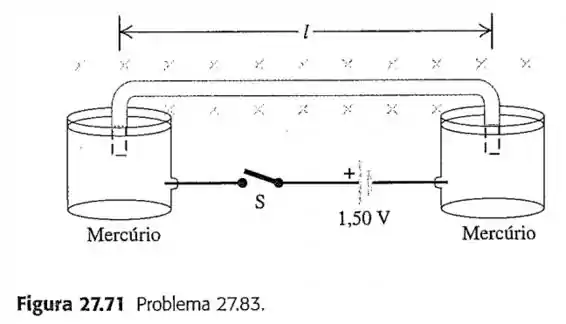
83- Um fio de arame isolado com massa é encurvado, formando um invertido, de tal modo que a parte horizontal possui comprimento . As extremidades encurvadas do fio são parcialmente imersas em dois recipientes cheios de mercúrio, e cada extremidade fica abaixo da superfície do mercúrio.

A estrutura inteira está em uma região onde existe um campo magnético uniforme de direcionando para o interior da página (Figura ). Uma ligação elétrica dos recipientes de mercúrio se dá através das extremidades dos fios. Os dois recipientes de mercúrio são conectados a uma bateria de e a uma chave . Quando a chave está fechada, o fio salta para o ar, a partir de sua posição inicial.

Determine a velocidade do fio quando ele deixa o mercúrio.

Supondo que a corrente , que passa no fio, permaneça constante desde o momento em que a chave foi fechada até o instante em que o fio sai do mercúrio, determine o valor de .

Desprezando as resistências dos fios do circuito e a resistência do mercúrio, determine a resistência do fio de arame.

Agora precisamos descobrir a força magnética que será causada nesse fio a ponto de fazer-lo voar com a corrente que passa sobre ele. E para isso vamos precisar entender o diagrama de forças nesse corpo.

A corrente sempre sai do terminal positivo da bateria, e como ela segue todo esse sentido então pela regra da mão esquerda vemos que a força magnética do corpo aponta na direção para, enquanto a força peso aponta para baixo, a resultante nos dá uma aceleração para cima de modo a termos o seguinte desenho.

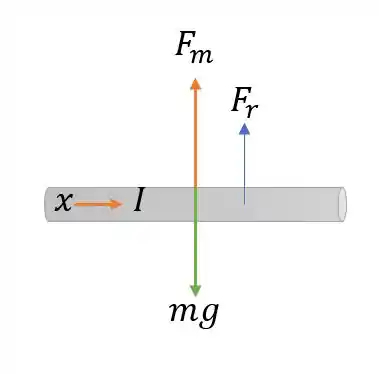
Então:

Onde é a aceleração do fio do começo até quando ele sai do mercúrio (como dito na letra ) então por Torricelli de novo nós teremos:

Pois ele parte do repouso e chega até que é quando ele sai do mercúrio.

Então:

Então pelo diagrama de corpo livre temos:

Substituindo os valores nós temos:

A resistência do fio de arame que está conectado em série com a bateria é de: