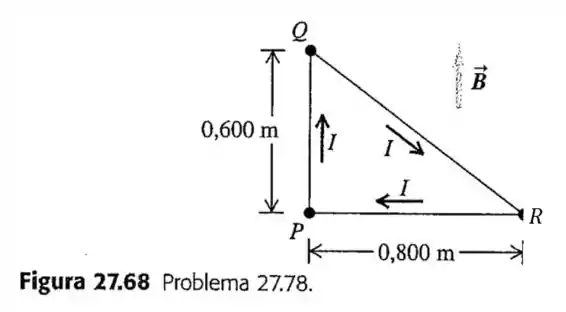
78- A espira triangular de fio indicada na Figura transporta uma corrente no sentido indicado. A espira está em um campo magnético uniforme com módulo e o mesmo sentido da corrente que passa pelo lado da espira.
Determine a força exercida pelo campo magnético em cada lado do triângulo. Se a força for diferente de zero, especifique a sua direção e sentido.
Qual é a força resultante que atua sobre a espira?
A espira revolve em torno de um eixo que fica ao longo do lado . Use as forças obtidas no item para determinar o torque sobre cada lado da espira (veja Problema ).
Qual é o módulo do torque resultante sobre a espira? Calcule o torque resultante a partir do torque resultante a partir dos torques obtidos no item e também de acordo com a Equação . Esses resultados se equivalem?
O torque resultante está orientado para girar o ponto para dentro do plano da figura ou para fora desse plano?
Passo 1
Por estar no mesmo sentido da corrente no lado nós temos que a força nesse lado de forma vetorial será:
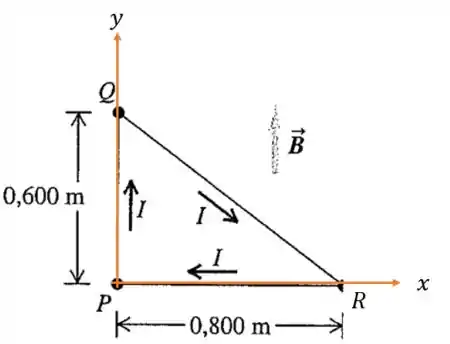
Considerando o seguinte sistema de coordenadas.
Então a força no lado será:
Sentido a entrar para dentro da página. Pois o vetor tem que respeitar o sentido da corrente, que no caso da reta é contra o eixo x.
Já para temos:
Sentido para fora da página.
E a força resultante que atua na espira toda é a soma de todas as forças que atuam sobre ela, ou seja:
Então a força na espira toda é nula.
Passo 2
De modo vetorial nós temos que o torque é dado por:
Como a articulação está ao longo do lado e no lado não temos nenhuma força (portanto nenhum torque), então a única força que geraria momento é a força no lado de modo que temos:
Pois a força se localiza no meio geométrico da reta.
Então:
E pelo eixo de rotação estar no eixo , então somente teremos momento no eixo , resistindo a qualquer outro torque então:
Passo 3
Pela equação para a letra temos:
Onde é o ângulo entre o eixo da espira e a direção do campo e elas são perpendiculares para toda a espira então.
O que condiz com o que foi encontrado no passo 2.
A força no meio da reta está no sentido para fora da página fazendo momento na reta, e provocando giro na reta então ela tenderá a fazer com que saia da página também/