Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 27.1 - Ex. 97

Um disco não condutor de raio R possui uma densidade superficial uniforme de cargas iguais e gira com uma rapidez angular omega. Considere uma faixa angular de raio R, espessura de R e carga dq . Mostre que a corrente dele produzido por esta faixa girando é dada por .O seu resultado da partida para mostrar que a intensidade do campo magnético no centro do disco é dada pela expressão. Se use seu resultado da parte a para determinar uma expressão para intensidade do campo magnético em um ponto no eixo central do Disco a uma distância z de seu centro.

Passo 1

O diagrama mostra o disco giratório e a faixa circular de raio r e largura dr com dq. Podemos usar a definição de densidade de carga superficial para expressar dq em termos de r e dr e a definição atual para mostrar que . Nós podemos então usar esta corrente e a expressão para o campo magnético no eixo de um anel atual para obter os resultados para nas partes (b) e (c).

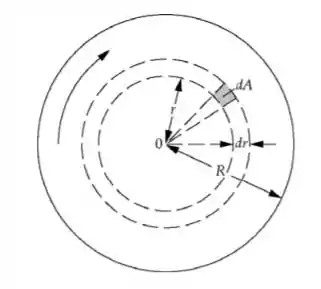
Letra a:

dq é:

d q = σ d A = 2 π σ r d r

E dl:

d I = d q d t = 2 π σ r d r 2 π ω = ω σ r d r

Passo 2

Letra b:

Avalie B x com x = 0 :

B x 0 = μ 0 ω σ 2 R 2 R 2 = 1 2 μ 0 σ ω R

Passo 3

Letra c:

d B x = μ 0 4 π 2 π r 2 d I z 2 + r 2 3 2

d B x = μ 0 ω σ r 3 2 z 2 + r 2 3 2   d r

Vamos integrar de r = 0 a r = R para obtermos:

d B x = μ 0 ω σ 2 ∫ 0 R r 3 z 2 + r 2 3 2 d r  

B x = μ 0 ω σ 2 R 2 2 ^ 2   R 2 + z 2 - 2 x

Resposta

Vide o passo a passo.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na figura 29-49a mostra, em seção reta, dois fio longos e paralelos, percorridos por correntes e separados por uma distância L . A razão i 1 / i 2 entre as correntes é 4,00 ; os sentidos das correntes
A figura 29-56 quatro fios retilíneos longos são perpendiculares ao pael e suas seções retas formam um quadrado de lado a = 20c m . As correntes são para fora do papel nos fios 1 e 4 para dentro do pa
Na figura 29-58, a = 4,7c m e i = 13A . Determine (a) o módulo e (b) o sentido (para dentro ou para fora do papel) do campo magnético no ponto P.
A figura 29-61 mostra, em seção reta, dois fios retilíneos longos apoiados na superfície de um cilindro de plástico com 20,0c m de raio e paralelos ao eixo do cilindro. O fio 1 conduz uma corrente i 1
A figura 29-55a mostra dois fios. O fio 1 é formao por um arco de circunferência de raio R e dois segmentos radiais e conduz uma corrente i 1 = 2,0A no sentido indicado. O fio 2 é longo e retilíneo, c