Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 7.Exercícios e Problemas - Ex. 4

7.4P A figura 7.14 mostra um reservatório cilíndrico cujas paredes têm espessura e densidade uniformes. O reservatório em massa m r e contém uma massa m a de água. Determine a posição do centro de massa do sistema, supondo que a espessura das paredes do reservatório seja muito menor do que as outras dimensões do sistema.

Passo 1

Belezoca galerinha, nossa figura 7.14 representa o reservatório como:

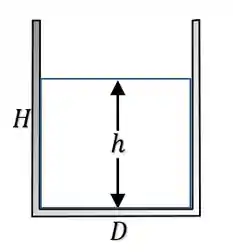
E a fórmula pro cálculo do centro de massa é dada por:

h c m = 1 M ∑ i = 1 n m i r i  

Onde:

M = ∑ i = 1 n m i

Belezoca, e temos apenas a massa m r do reservatório e massa m a da água contida dentro dele, tal que:

M = m r + m a

Então com toda sagacidade do mundo, nossa equação se torna:

h c m = 1 M ∑ i = 1 n m i r i = m r h r + m a h a m r + m a

Onde h r e h a são as posições do centro de massa do reservatório (vazio) e da coluna de água. Então só precisamos encontrar esses valores pra executar nosso plano infalível.

Passo 2

Saca só, se hipoteticamente nosso reservatório estivesse vazio, seu centro de massa seria calculado apenas pelas laterais e pela base do cilindro que forma o reservatório. A área da base desse cilindro será dada por:

A b = π r 2

Onde r é o raio da base, mas como no nosso desenho podemos ver que o diâmetro do cilindo é igual a D , então teremos que:

r = D 2

Logo:

A b = π D 2 4

Belezoca, agora a área da lateral do cilindro pode ser calculada como se fosse a área de um retângulo, onde a lateral do retângulo é a altura H , enquanto a base do retângulo é a circunferência da base do cilindro tal que:

A L = a l t u r a   r e t â n g u l o × b a s e   r e t â n g u l o

A L = H × 2 π D 2

Logo a área da lateral é:

A L = π D H

E como o reservatório é homogêneo e sua espessura pode ser desprezada, podemos dizer que ele possui uma densidade uniforme ρ r tal que a massa da base e a massa da lateral é:

m b = ρ r π D 2 4 ,     m L = ρ r π D H

Portanto a massa total desse sistema é:

m T = m b + m L

m T = ρ r π D 2 4 + D H

Passo 3

Feshow de bola, então o centro de massa do reservatório vazio vai ser dado por:

h r = m b 0 + m L H 2 m b + m L

Logo:

h r = 0 + ρ r π D H H 2 ρ r π D 2 4 + D H

h r = D H 2 2 D 2 + 4 D H 4

h r = 2 D H 2 D 2 + 4 D H

Portanto o centro de massa do reservatório vazio é dadoi por:

h r = 2 H 2 D + 4 H

Passo 4

Iradoso, então quer dizer que nosso centro de massa do reservatório cheio pode ser medido como:

h c m = m r h r + m a h a m r + m a

Onde h a é a altura média da coluna de água, onde se encontra se centro de massa h a = h 2 , logo nossa equação se torna:

h c m = m r 2 H 2 D + 4 H + m a h 2 m r + m a

Resposta

h c m = m r 2 H 2 D + 4 H + m a h 2 m r + m a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

7.3P Determine a posição do centro de massa do hemisfério homogêneo de raio R , visto na Figura 7.13.
7.25P Calcule o centro de massa de um sistema de quatro partículas iguais dispostas nos vértices de um quadrado de lado L .
60 . Mudando seu centro de massa. Para manter os cálculos bem simples, mas ainda razoáveis, modelamos o membro inferior do corpo humano que possui 92,0c m (medidos a partir do quadril), supondo que a
Na Seção 8.5, calculamos o centro de massa considerando objetos compostos por um número finito de massas puntiformes ou objetos que, por simetria, pudessem ser representados por um número finito de ma
CALC Use os métodos do Problema desafiador 8.104 para determinar as coordenadas x e y do centro de massa de uma placa metálica semicircular com densidade uniforme e espessura t. Chame de a o raio da p