Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 8.5 - Ex. 60
. Mudando seu centro de massa. Para manter os cálculos bem simples, mas ainda razoáveis, modelamos o membro inferior do corpo humano que possui (medidos a partir do quadril), supondo que a coxa e a parte inferior desse membro (que inclui a perna e o pé) possuem tamanhos iguais e são uniformes. Para uma pessoa de , a massa da coxa é de , enquanto a massa da parte inferior desse membro (incluindo a perna e o pé) é de . Ache o local do centro de massa do membro inferior do corpo humano, em relação ao quadril, quando o membro inferior estiver esticado horizontalmente e encurvado no joelho formando um ângulo reto, com a coxa permanecendo na horizontal.
Passo 1
Vamos olhar para o desenho abaixo que está simbolizando a perna em cada posição. Reparem que definimos coordenadas para melhor entendimento na hora de resolver o exercício.
Ahh, outra coisa que podemos considerar na questão pra facilitar é imaginar que massa de cada parte da perna está concentrada no centro de massa dessa parte. Não entendeu? Um jeito mais simples de dizer é que toda massa da coxa ( como dito no enunciado) está concentrada exatamente no meio da coxa, vamos ter o mesmo pensamento em relaão a parte inferior do membro.
Observe o desenho abaixo e confere se faz sentido!
É sempre importante olhar o desenho pra entender o que tá acontecendo.
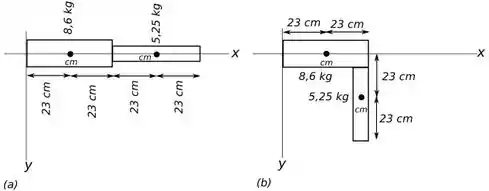
Agora vamos encontrar as posições do centro de massa em cada situação, vem comigo!
Passo 2
Nessa primeira situação a perna está toda esticada, ou seja, na horizontal. Isso significa que , então o único que teremos que calcular é o .
Sabemos que:
Lembrando que e são as massas da coxa e da parte inferior do membro, respectivamente e que e são as coordenadas de e , respectivamente.
Colocando os valores temos:
Ou seja, o centro de massa da perna está a uma distância horizontal de do quadril
Passo 3
Agora que vamos fazer para outra situação no que o centro de massa vai ter componentes e . Vamos calculá-los então:
Resposta
e
e