Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 8.Problemas - Ex. 105
CALC Use os métodos do Problema desafiador 8.104 para determinar as coordenadas x e y do centro de massa de uma placa metálica semicircular com densidade uniforme e espessura t. Chame de a o raio da placa. Então, a massa da placa é M 1 2 rp a2 t. Use o sistema de coordenadas indicado
Passo 1
Vamos fazer mais uma questão!!
E aiii galera,
Temos o seguinte:
Na superfície superior da placa,
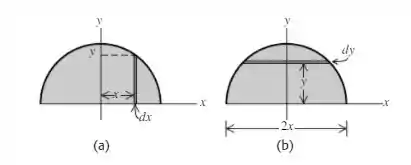
Para encontrar , divida a placa em tiras finas paralelas ao eixo y, como mostrado na figura a. Então, encontre , divida a placa em tiras finas paralelas ao eixo x, conforme mostrado na figura b.
A placa tem o volume de metade de um disco circular, então
Passo 2
Na figura a, cada tira tem comprimento .
onde .
Então, , uma vez que o integrando é uma função ímpar de x. devido à simetria.
Na figura b, cada tira tem comprimento .
, onde
Passo 3
Então,
A integral pode ser avaliada usando:
E substituindo temos:
. é menor que , como esperado, uma vez que a placa se torna mais larga à medida que y diminui.