75. Como hobby, você gosta de participar de encenações de batalhas da Guerra Civil Norte-Americana. Os canhões daquela época eram “carregados pela boca”, no sentido de que uma carga de pólvora e uma bola de canhão eram inseridas pela saída da arma e, depois, pressionadas com um longo pilão. Para recriar os canhões autênticos carregados pela boca, mas sem o perigo dos canhões de verdade, os atores da encenação da Guerra Civil inventaram um canhão em que uma mola arremessa uma bola de plástico de . Uma mola, de constante elástica igual a , é fixada na extremidade traseira do cano. Você coloca uma bola dentro do cano, depois usa um longo pilão para pressionar a bola contra a mola a fim de armar a mola na posição correta, pronta para disparar. Para engatar o gatilho da mola, a bola deve estar se movendo com, no mínimo, quando a mola estiver comprimida em . O coeficiente de atrito cinético da bola com o cano é de . O pilão não toca a lateral do cano.
a. Se você empurra o pilão com uma força constante, qual é o mínimo valor de força que deve comprimir a mola até engatar a mola? Considere que nenhum esforço seja necessário para empurrar a bola cano abaixo até que ela faça contato com a mola pela primeira vez.
b. Quanto vale a velocidade da bola na boca do canhão se ela percorre uma distância total de até a extremidade do cano?
Passo 1
Bom! A melhor forma de se começar resolvendo esse problema, é fazer um esboço do que está acontecendo em nosso problema.
A imagem abaixo, retrata o que está acontecendo tanto na letra quanto na , desse problema...
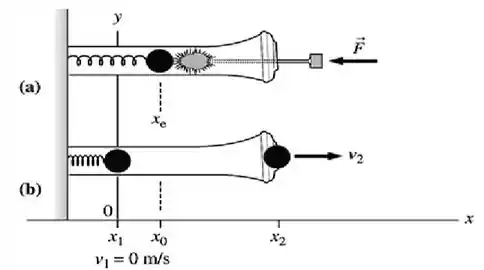
Passo 2
a) Sendo assim, vamos a esse primeiro item...
Se liga só! Vamos usar conversação da energia pra resolver essa primeira parte...
Bom! Pelo que lemos do enunciado... Graças ação de uma força , a mola vai ser comprimida da posição até , onde a bola vai estar com velocidade de .
Mas não podemos esquecer que o contato entre o cano e a bola tem atrito.
Sendo assim, a energia inicial não é igual a final. Pelo contrário, o trabalho da força menos o trabalho dissipativo da força de atrito será igual a energia quando a mola estiver comprimida e a bola com velocidade de .
Logo,
Como e ... Então;
Conseguimos obter finalmente a nossa força de compressão!
Passo 3
b) Já para esse segunda letra, novamente vamos se aproveitar das relações de energia.
Bem! A bola que entra no cano fazendo a bola se comprimir, não vai estar mais com uma velocidade de . A velocidade de foi no início da compressão.
Quando a compressão terminou, a bola já vai estar com uma velocidade nula, pronta para ser rebatida de volta. Considerando esse momento, como o inicial para a nossa análise, a energia presente nele vai ser...
Nosso cano tem atrito, né não!? Sendo assim, essa energia inicial vai ser dissipada pela presença do atrito, cuja energia de dissipação vale...
Por fim, após percorrer o tubo, a bolinha sai com uma velocidade tal, que chamaremos de . Nesse instante, a energia cinética é a única presente.
Adquirimos então, a seguinte relação...
Como ...
Pronto! Essa é a velocidade da bola quando sai do cano!
Resposta
a)
b)