Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 55
Partindo do repouso, uma caixa de plástico de desce deslizando uma elevação sem atrito e com de altura, atravessa uma superfície horizontal com de comprimento e depois colide com uma mola horizontal de constante elástica igual a .
A outra extremidade da mola está ancorada a uma parede. O solo sob a mola é desprovido de atrito, porém a superfície horizontal de de largura é áspera, sendo de o coeficiente de atrito cinético do caixote com a mesma.
a. Qual é o valor da velocidade da caixa imediatamente antes de atingir o trecho áspero?
b. Qual é o valor da velocidade da caixa imediatamente antes de colidir com a mola?
c. Em quanto será comprimida a mola?
d. Incluindo a primeira travessia, quantas percursos completos a caixa efetuará através do trecho áspero antes de parar?
Passo 1
Vamos desenhar a situação antes do bloco descer e depois do bloco se colidir com a mola
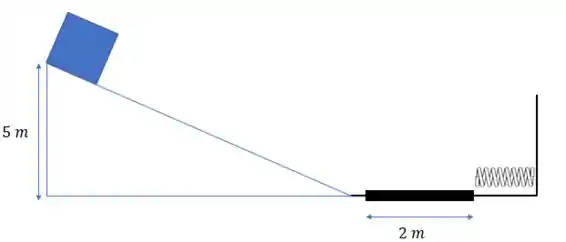
De forma que nesse estado somente temos a energia potencial gravitacional (considere a altura do centro da caixa até o piso igual a ), o que nos dá uma energia mecânica de:
E antes de atingir a região áspera nós temos a total conversão de energia potencial gravitacional em energia cinética uma vez que ele chega numa região de altura zero e ainda não tem atrito.
Portanto:
Passo 2
Exatamente antes de colidir com a mola o bloco passa por um terreno áspero que faz com que uma parte da energia cinética seja perdida então:
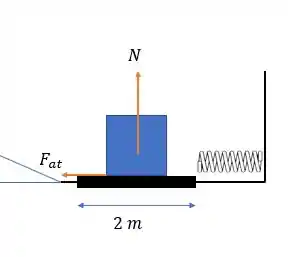
Onde será nesse caso apenas o trabalho da força de atrito (que age contra o movimento do bloco) então a velocidade final desse bloco após será de:
Substituindo os valores que o enunciado nos fornece teremos:
E essa será a velocidade do bloco após percorrida todo o terreno áspero e entrar em contato com a mola. (resposta da letra )
Passo 3
E com isso essa nova energia cinética entra em contato com a mola e transfere toda a energia cinética em energia potencial elástica de modo que a compressão na mola seja de:
Passo 4
Agora para a letra vemos que o sistema começa com de energia e termina com a compressão da mola com:
Então uma travessia faz ele perder de energia
Isso nos dá um número de travessias igual a:
Ele quase termina a décima travessia (isso é por que consideramos e não , fazendo isso dá 10 certinho), podemos entender esse número como 5 idas e 5 voltas desse cubo