Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 29.Exercício - Ex. 36
36- Um capacitor de placas paralelas e cheio de ar está sendo carregado, como indica a Figura . As placas circulares possuem raio de e, em um dado instante, a corrente de condução nos fios é de .
Qual é a densidade de corrente de deslocamento no espaço entre as placas?
Qual é a taxa de variação do campo elétrico entre as placas?
Qual é o campo magnético induzido entre as placas a uma distância de do eixo?
E a cm do eixo?
Passo 1
Sabendo que a corrente de deslocamento é igual a corrente de condução então a densidade de corrente para esse capacitor que têm placas circulares então:
E outra forma de ver a densidade de corrente de deslocamento é:
Onde então:
Já respondemos as letras e , veja só você.
Passo 2
Já a letra e precisa-se de um certo raciocínio, pois a distância fora do eixo desse ‘’cilindro’’ nos dá:
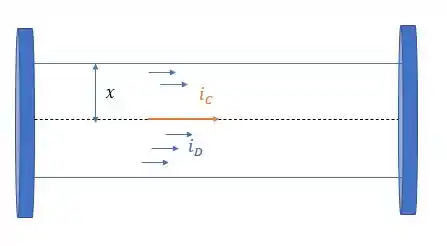
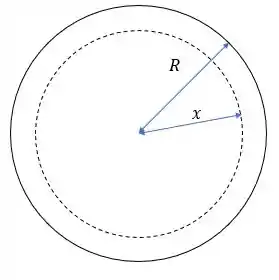
Então pela lei de Ampere temos:
A corrente de condução flui somente no meio entre as placas, no eixo, não a uma distância do eixo, o que flui nessa direção e a corrente de deslocamento.
Porém não podemos colocar o seu valor total, e sim somente o valor que está dentro daquela área específica e que será .
Essa é a principal graça da corrente de deslocamento, pois é a corrente que flui no corpo todo, e é proporcional a área de análise. A corrente de condução pode ser vista como a soma de toda a corrente de deslocamento no corpo todo.
Para temos.
E para