125- Aproximadamente kg de água caem das Cataratas do Niágara por segundo.
(a) Qual é o decréscimo da energia potencial gravitacional do sistema água-Terra por segundo? (b) Se toda essa energia pudesse ser convertida em energia elétrica (o que não é possível), a que taxa a energia elétrica seria produzida? (A massa de de água é 1000 kg.)
(c) Se a energia elétrica fosse vendida a 1 centavo de dólar/kW·h, qual seria a receita anual?
Passo 1
- Dando um google conseguimos ver que a altura dos cataratas do Niágara vale:
- A potência é calculada pela seguinte forma:
- Como queremos saber a receita anual dessa energia nós precisamos saber quantas horas há em um ano, já que o ganho está em , logo:
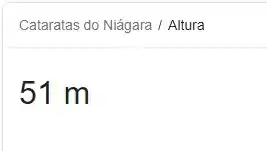
Logo em segundo temos uma variação de energia igual a:
Passo 2
Porém como nos é dito no enunciado que existe uma queda de água por segundo então temos:
Passo 3
Já que um dia tem
Além de que a energia que encontramos tem que estar em não em . Para isso basta dividir por 1000.
Agora podemos ter nossa receita: