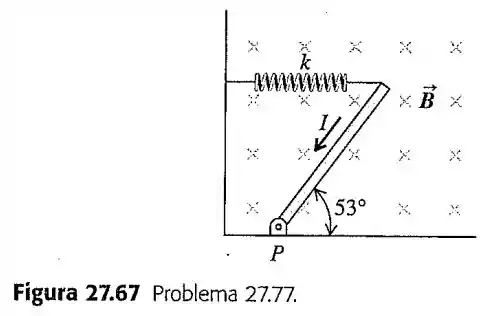
77- Uma barra delgada uniforme, com massa desprezível e comprimento de , está fixa no solo por uma dobradiça de atrito desprezível no ponto (Figura ). Uma mola horizontal, com constante de força , conecta a outra extremidade do bastão a uma parede vertical. O bastão está em um campo magnético uniforme orientado para dentro do plano da figura. Uma corrente passa pelo bastão, no sentido indicado.
Calcule o torque em função da força magnética sobre o bastão, para um eixo no ponto . É correto tomar a força magnética total para atuar no centro de gravidade do bastão, ao calcularmos o torque? Explique
Quando o bastão está em equilíbrio e forma um ângulo de em relação ao solo, a mola está estendida ou comprimida?
Quanta energia é armazenada na mola, quando o bastão está em equilíbrio?
Passo 1
Tomando um elemento infinitesimal da barra nós teremos a seguinte força magnética atuando na barra.
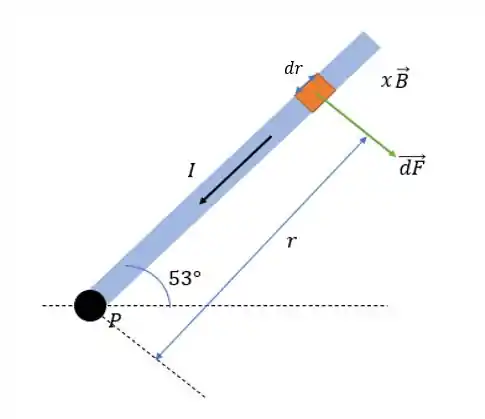
Onde o elemento de força será igual a:
Então o torque em será:
O que nos dá (se preocupando apenas com o escalar do torque) uma intensidade de momento igual a:
Como e varia de até então teremos um valor de torque igual a:
Até daria para calcular a força magnética total no meio da barra , se liga no que a integral nos deu:
A parcela é a área de toda a força magnética e nos diz que essa força está no meio da espira. Porém a chance de você errar isso sem a análise da integral é bem alta.
Passo 2
A força magnética tende a puxar a barra para a direita então é bem provável que a mola esteja esticada puxando o sistema para o outro lado.
De forma que o sistema de forças nessa barra seja.
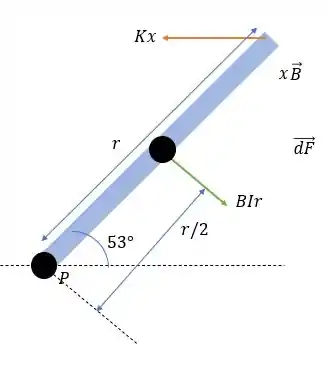
O equilíbrio de momentos nessa barra será igual a:
Então a energia armazenada nessa mola será de: