Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 27.Problemas desafioadores - Ex. 91
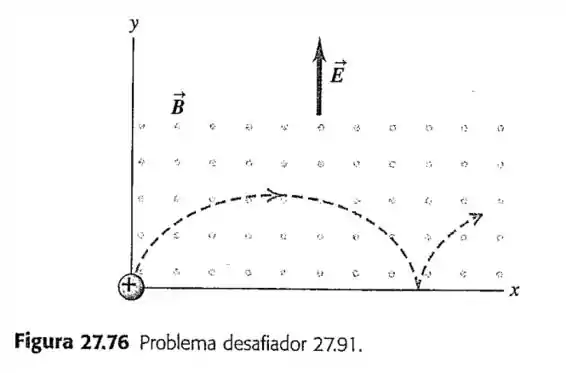
91- Uma trajetória cicloidal. Uma partícula de massa e carga positiva parte do repouso na origem na Figura . Existe um campo elétrico uniforme no sentido e um campo magnético uniforme saindo da página. Demonstra-se em livros mais avançados que a trajetória descrita é uma cicloide, cujo raio de curvatura nos pontos do topo da curva é igual ao dobro da coordenada desses pontos.
Explique a razão desse tipo de trajetória e o motivo da repetição do movimento.
Prove que a velocidade em qualquer ponto é dada por . (Sugestão: use conservação da energia).
Aplicando a segunda Lei de Newton no ponto do topo da trajetória e levando em conta a informação de que nesse ponto o raio de curvatura é igual a , prove que a velocidade nesse ponto é igual a .
Passo 1
O campo elétrico tende a puxar a partícula na direção positiva de , fazendo com que ela ganhe aceleração para a direita(pela força magnética) e para cima, com isso a força magnética tende a mover a carga para acelerar a carga para direita e o campo elétrico para mover a partícula para cima.
Porém como a partícula começa a mover-se para a direita também cria-se uma força magnética para baixo que se opõe com a força elétrica e a velocidade na horizontal e na vertical terão o mesmo valor por conta disso.
E a medida que a partícula acelera para cima com o campo elétrico nós teremos o crescimento da força magnética para baixo, fazendo com que a força magnética que aponta para baixo cresça a ponto de ser maior que a força elétrica (no ponto mais alto da partícula), acelerando a partícula para baixo (mantendo a velocidade da partícula para a direita, mesmo que haja outra parcela que puxe a carga para a esquerda, que é mais fraca). Então quando a força magnética cessa e o campo elétrico faz com que a partícula volte a ter o mesmo comportamento.
Passo 2
O trabalho que a partícula faz no seu trajeto é o mesmo que a sua energia cinética, uma vez que qualquer ganho de energia potencial possa ser desconsiderada aqui, então:
Como o trabalho é inteiramente causado pela força elétrica fazendo com que a partícula percorra uma distância então:
Passo 3
No ponto máximo da trajetória temos a seguinte situação:
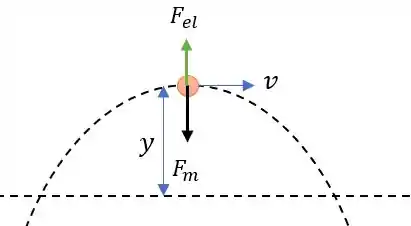
Onde a força magnética se opõe a força elétrica, mudando a aceleração da partida , então no topo da trajetória temos ação da força centrípeta da partícula que tende a apontar a força para baixo (na direção da força magnética) nos dando a seguinte conta:
Como então:
Substituindo teremos:
Resposta
Ei, a resposta está no passo a passo :)