Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 26.Problemas - Ex. 54

Necessitamos de um resistor de 400   Ω e 2,4   W , porém dispomos apenas de alguns resistores de 400   Ω e 1,2   W . (Veja o Exercicio 26.10.) (a) Quais são as duas combinações de resistores disponíveis que fornecem a resisencia e a potencia desejadas? (b) Sabendo que essas combinações dissipam uma potencia total de 2,4   W , qual é a potencia dissipada em cada resistor para cada combinação determinada no item (a)?

Passo 1

  1. Dois dos resistores em série dissipariam metade do total, ou 1,2   W , o que é bom. Mas

    2. a combinação de séries teria uma resistência equivalente a 800   Ω , não a 400   Ω necessária. Resistores em paralelo tem uma resistência equivalente menor que a dos resistores individuais, então uma solução é duas em série em paralelo com outros dois em série.

    A rede pode ser simplificada como mostra a Figura:

     

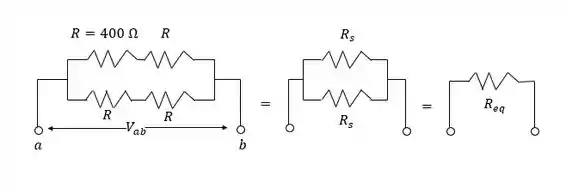
    Passo 2

    R s é a resistência equivalente a dois dos resistores de 400   Ω em série.

    R s = R + R = 800   Ω  

    R e q é a resistência equivalente aos dois R s = 800   Ω   resistores em paralelo:

    1 R e q = 1 R s + 1 R s = 2 R s ;

    R e q = 800   Ω 2 = 400   Ω .

    Essa combinação possui a resistência equivalente a 400   Ω necessária. Será mostrado na parte (b) que um total de 2,4   W pode ser dissipado sem exceder a potência nominal de cada resistor individual.

    Passo 3

  2. Encontre a tensão aplicada V a b de modo que um total de 2,4   W seja dissipado e, em seguida, V a b encontra a potência dissipada por cada resistor.

Para uma combinação com resistência equivalente R e q = 400   Ω para dissipar 2,4   W a tensão V a b aplicado à rede deve ser fornecido por

P = V a b 2 R e q

Então

V a b = P R e q = 2,4   W ⋅ 400   Ω = 31,0   V

e a corrente através da resistência equivalente é

I = V a b R = 31,0   V 400   Ω = 0,0775   A .

Passo 2

Para a primeira combinação, isso significa 31,0   V   através de cada ramo paralelo e ½   ( 31,0   V ) = 15,5   V através de cada resistor 400   Ω .

A energia dissipada por cada resistor individual é então

P = V 2 R = 15,5   V 2 400   Ω = 0,60   W

 que é menor que o valor máximo permitido de 1,20   W . Para a segunda combinação, isso significa uma tensão de

I R p = 0,0775   A 200   Ω = 15,5   V

Passo 3

através de cada combinação paralela e, portanto, através de cada resistor separado. A energia dissipada por cada resistor é novamente

P = V 2 R = 15,5   V 2 400   Ω = 0,60   W ,

é menor que o valor máximo permitido de 1,20   W .

A simetria de cada rede diz que cada resistor na rede dissipa a mesma energia. Então,

para um total de 2,4 W dissipados pela rede, cada resistor se dissipa

2,4   W 4 = 0,60   W ,

o que concorda com a análise acima.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

70- Três resistores idênticos são conectados em série. Quando uma certa diferença de potencial é aplicada através da combinação, a potência total dissipada é igual a 27W . Qual seria a potência total
Os fios em uma casa devem ter diâmetro grande o suficiente para não ficarem muito quentes a ponto de iniciarem um incêndio. Enquanto você trabalha para um construtor durante o verão, você se envolve n
O fio C e o fio D são feitos de materiais diferentes e têm comprimentos L_c = L_D = 1,0 m. A resistividade e o diâmetro do fio C são 2,0 times 10^-5 %OMEGA ·m e 1,00 mm e a resistividade e o diâmetro
Uma lâmpada de 100 W é ligada a uma tomada de parede de 120 V. (a) Quanto custa deixar a lâmpada ligada continuamente durante um mês de 31 dias? Suponha que o preço da energia elétrica é $0,06/kW · h.
Um desfibrilador cardíaco é usado para permitir que o coração comece a bater novamente depois de parar. Isso é feito passando uma grande corrente de 12A através do corpo, a 25V durante um tempo muito