Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 27.Exercício - Ex. 22
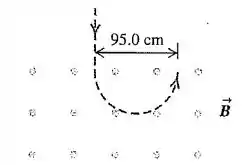
Em uma experiência com raios cósmicos, um feixe vertical de partículas que possuem carga com módulo e massa 12 vezes maior que a massa do próton penetra em um campo magnético horizontal uniforme de 0,250 T e está encurvado em um semicírculo com diâmetro igual a 95,0 cm, como indica a Figura 27.47.
- Calcule a velocidade escalar das partículas e o sinal da sua carga.
- É razoável ignorar a força da gravidade sobre essas partículas?
- Como a velocidade escalar das partículas quando elas penetram no campo se compara à sua velocidade ao saírem do campo?
Passo 1
letra a)
Como a partícula descreve um movimento circular. Então vamos igualar força magnética com força centripeta.
Como o campo e a velocidade são perpendiculares, :
Isolando a velocidade:
Pela regra da mão direita, a carga é negativa.
Passo 2
letra b)
A força magnética tem magnitude maior que a força peso, porque a massa da partícula é muito pequena. Então a peso pode ser ignorada.
Passo 3
letra c)
A força magnética não altera a magnitude da velocidade. A velocidade é constante.
Resposta
letra a), carga negativa.
letra b) É razoável.
letra c)velocidade constante.