Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 17.Problemas Adicionais - Ex. 103
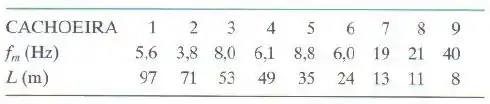
Acústica das cachoeiras. O impacto turbulento da água de uma cachoeira faz o solo oscilar em uma larga faixa de baixas frequências. Se a água cai livremente (em vez de bater nas pedras enquanto desce), as oscilações são maiores em uma frequência particular . Este fato sugere que o fenômeno se deve a uma ressonância acústica e que é a frequência fundamental. A tabela a seguir mostra, para nove cachoeiras americanas e canadenses, os valores medidos de e da altura da queda livre da água. Mostre como representar os dados em um gráfico para obter a velocidade do som na água da cachoeira. A partir do gráfico, calcule a velocidade do som se a ressonãncia for como a ressonãncia em um tubo (a) com a duas extremidades abertas e (b) com apenas uma extremidade aberta. A velocidade do som em uma água turbulenta contendo bolhas de ar pode ser cerca de menor que a sua velocidade de em água parada. (c) A partir das respostas dos itens (a) e (b), determine quantas extremidades abertas estão efetivamente envolvidas na ressonância de uma cachoeira.
Passo 1
Já que vamos modelar a ressonância como se acontecesse em um tubo, é interessante fazer um gráfico de em função do inverso de , já que as fórmulas para as frequências de ressonância dos tubos são:
Ou seja, aparece no denominador nos dois casos. O gráfico fica da seguinte forma:
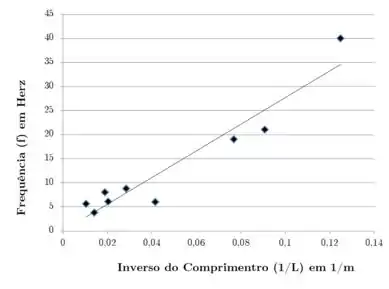
E usando o método dos mínimos quadrados para ajustar uma reta a esses dados, ficamos com a seguinte equação:
Passo 2
(a) No caso em que modelamos esse sistema como um tubo com as duas extremidades abertas em , temos:
Nesse caso, teríamos que desprezar o coeficiente linear , e fazer a seguinte igualdade por comparação:
Passo 3
(b) No caso em que modelamos esse sistema como um tubo em que apenas uma extremidade está aberta:
Então, pela mesma lógica de antes, encontramos o seguinte:
Passo 4
(c) A velociade calculada no item (b) é significativamente mais próxima da velocidade de que foi mencionada no enunciado.
Portanto, podemos estimar que esse problema é melhor modelado como um tubo que tem apenas uma extremidade aberta.
Resposta
(a) .
(b) .
(c) Uma extremidade aberta.