Exercícios de Tubos Sonoros - Lista de Exercícios Resolvida

No tubo , a razão entre a frequência de um certo harmônico e a frequência do harmônico precedente é 1,2. No tubo , a razão entre a frequência de um certo harmônico e a frequência do harmônico precedente é . Quantas extremidades abertas existem (a) no tubo e (b) no tubo ?

Considere dois tubos de ar de mesmo comprimento e mesma seção transversal, um deles fechado numa das extremidades, e o outro, aberto em ambas, e ondas sonoras propagando-se nestes tubos. Considere as afirmações abaixo:

O deslocamento é máximo na extremidade do tubo aberto pois há um máximo de onda de pressão neste ponto.

O deslocamento é máximo na extremidade do tubo aberto pois há um nodo da onda de pressão neste ponto.

O comprimento de onda do modo fundamental, no tubo fechado, é o dobro do comprimento de onda deste modo no tubo aberto.

O comprimento de onda do modo fundamental, no tubo aberto, é o dobro do comprimento de onda deste modo no tubo fechado.

Qual(is) da(s) afirmação(ões) acima é(são) verdadeira(s)?

1. .
2. e .
3. e
4. e
5. e
6. e
7. e .

A figura mostra uma “‘flauta” simplificada, com a extremidade aberta. Há também uma grande abertura em (próxima ao bocal) e dois orifícios em e , tais que e . Sabe-se que e que a velocidade do som é Qual a frequência que se espera ouvir ao soprar a flauta com o dedo tapando ?

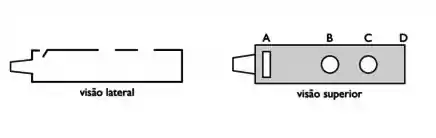
2. Não há como excitar uma onda no tubo, já que e estão à mesma pressão externa.
3. .
4. .
5. .

Um tubo , que possui de comprimento e é aberto em suas duas extremidades, vibra na sua terceira frequência harmônica mais baixa. Outro tubo , de comprimento , é fechado em uma de suas extremidades e vibra em sua segunda frequência harmônica mais baixa. As frequências dos tubos e coincidem. Dado:

1. Encontre as posições do tubo em que estão os nós de deslocamento.
2. Encontre o comprimento do tubo .

Um pequeno alto-falante é alimentado por um oscilador de áudio com uma frequência que varia de a . Um tubo cilíndrico tem de comprimento e as duas extremidades abertas, e é colocado próximo ao alto-falante. A velocidade do som no ar no interior do tubo é . Para quais frequências o som do alto-falante produz ressonância no tubo?

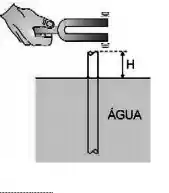
(B)Um tubo de vidro, aberto em ambas as extremidades, de diâmetro e comprimento , é colocado verticalmente na água de um tanque de modo que um pedaço do tubo fique fora da água e acima da linha da água. Faz se vibrar um diapasão na extremidade superior do tubo. Afunda-se o tubo, diminuindo-se lentamente , e verifica-se que os dois maiores valores de para os quais o som tem ampliação são e .

a) Escreva a relação entre e o comprimento de onda da onda sonora para que haja ressonância no tubo.

b) A que modos de vibração correspondem as duas ressonâncias em e ? Calcule a frequência do diapasão.

c) Calcule o(s) outro(s) valor(es) de em que haverá ampliação do som.

1. Um tubo de comprimento é fechado em uma extremidade Um fio de aço, de de comprimento e massa de , é esticado e colocado pra oscilar próximo à extremidade aberta do tubo. O fio, fixo nas duas extremidades, vibra numa frequência correspondente ao segundo harmônico. Essa vibração produz na coluna de ar dentro do tubo uma oscilação que corresponde ao primeiro harmônico. Considere a velocidade do som como
1. Encontre a frequência de oscilação da coluna de ar.
2. Desenha o tubo e faça uma representação transversal(tipo corda) dos nós e antinós de pressão para essa frequência.
3. Calcule a tensão no fio
4. Você está parado a uma distância de uma fonte pontual que emite ondas sonoras de forma isotrópica(igualmente em todas as direções). Ao caminhar em direção à fonte, observa que a intensidade foi dobrada.
2. Calcule a distância

Considere dois tubos de ar de mesmo comprimento e mesma seção transversal, um deles fechado numa das extremidades, e o outro, aberto em ambas, e ondas sonoras propagando-se nestes tubos. Considere as afirmações abaixo:

O deslocamento é máximo na extremidade do tubo aberto pois há um máximo de onda de pressão neste ponto.

O deslocamento é máximo na extremidade do tubo aberto pois há um nodo da onda de pressão neste ponto.

O comprimento de onda do modo fundamental, no tubo fechado, é o dobro do comprimento de onda deste modo no tubo aberto.

O comprimento de onda do modo fundamental, no tubo aberto, é o dobro do comprimento de onda deste modo no tubo fechado.

Qual(is) da(s) afirmação(ões) acima é(são) verdadeira(s)?

1. .
2. e .
3. e
4. e
5. e
6. e
7. e .

Um tubo , que possui de comprimento e é aberto em suas duas extremidades, vibra na sua terceira frequência harmônica mais baixa. Outro tubo , de comprimento , é fechado em uma de suas extremidades e vibra em sua segunda frequência harmônica mais baixa. As frequências dos tubos e coincidem. Dado:

1. Encontre as posições do tubo em que estão os nós de deslocamento.
2. Encontre o comprimento do tubo .

Um pequeno alto-falante é alimentado por um oscilador de áudio com uma frequência que varia de a . Um tubo cilíndrico tem de comprimento e as duas extremidades abertas, e é colocado próximo ao alto-falante. A velocidade do som no ar no interior do tubo é . Para quais frequências o som do alto-falante produz ressonância no tubo?

​Um tubo cilíndrico de comprimento consegue produzir ondas sonoras estacionárias apenas nas seguintes frequências: e no intervalo

Determine a frequência fundamental das ondas estacionárias no tubo, e se o tubo é aberto nas extremidades (aberto­aberto) ou se é aberto somente em uma (aberto­fechado).

Considere aqui a velocidade do som no ar de  

 aberto-aberto 

aberto-fechado 

aberto-aberto 

 aberto-fechado 

 aberto-aberto 

Uma corda de comprimento esticada tem uma extremidade mantida fixa () e a outra livre . Considere que, na configuração de equilíbrio, a corda se encontra na horizontal ao longo do eixo . Um aluno escreve que os pequenos deslocamentos transversais na direção podem ser representados pelos modos normais:

Onde = 1, 3, 5, ... , e são constantes a serem determinadas das condições iniciais do problema e é a velocidade de propagação da onda na corda. São feitas as seguintes observações sobre a solução apresentada:

1. Ela está incorreta, pois não obedece a condição de contorno .
2. Os modos pares com = 2, 4, 6,... também deveriam ter sido levados em consideração.
3. As condições de contorno para neste problema são as mesmas que uma onda sonora de deslocamento deve obedecer em um tubo de comprimento fechado em uma extremidade e aberto na outra.
4. Esta solução não representa uma solução da equação de onda, pois não pode ser escrita na forma, onde é uma constante real e e são funções de uma variável.

São verdadeiras:

1. Somente a (III).
2. Todas são verdadeiras.
3. Nenhuma é verdadeira.
4. Somente (I) e (II).
5. Somente (I) e (IV).
6. Somente (III) e (IV).
7. Somente (II) e (IV).
8. Somente a (IV)

Em um tubo de ressonância que e aberto numa extremidade e fechado na outra extremidade, há:

1. Nodos de deslocamento em cada extremidade.
2. Antinodos de deslocamento em cada extremidade.
3. Um nodo de deslocamento na extremidade aberta e um antinodo de pressão na extremidade fechada.
4. Um antinodo de deslocamento na extremidade aberta e um nodo de pressão na extremidade fechada.
5. Um nodo de deslocamento na extremidade fechada e um nodo de pressão na extremidade aberta.

Um tubo aberto-fechado produz um som que tem frequência fundamental de Se você abrir a parte fechada do tubo, qual será o novo valor da frequência fundamental?

Dois tubos estão abertos em uma extremidade e fechados na outra. O tubo tem comprimento e o tubo tem comprimento . Que harmônico do tubo corresponde à frequência fundamental do tubo ?

A) o segundo harmônico

B) o terceiro harmônico

C) o quarto harmônico

D) o quinto harmônico

E) não há nenhum

. Num tubo cheio de ar, onde a velocidade do som vale , observa-se que as três freqûencias ressonantes mais baixas são e . Podemos afirmar que:

Trata-se de um tubo de de comprimento, com uma extremidade aberta e a outra fechada.

Trata-se de um tubo de de comprimento, com suas duas extremidades abertas.

Trata-se de um tubo de de comprimento, com suas duas extremidades abertas.

Trata-se de um tubo de de comprimento, com uma extremidade aberta e a outra fechada.

Trata-se de um tubo de de comprimento, com uma extremidade aberta e a outra fechada.

Dois tubos de um órgão de tubos possuem comprimentos de , respectivamente. Ambos os tubos são abertos nas duas extremidades. Se os tubos ressonarem simultaneamente em seus modos fundamentais, qual é o número de batimentos (máximos de intensidade sonora) por segundo que uma pessoa nas proximidades dos tubos ouviria? Tome a velocidade do som como

1. 24
2. 12,5
3. 5
4. 12
5. 25

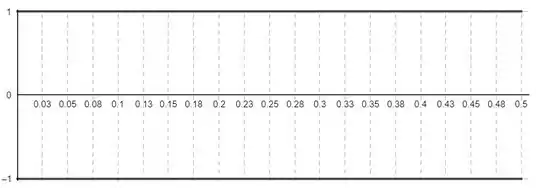
A figura abaixo mostra a leitura de um monitor de pressão montado em um ponto da trajetória de uma onda sonora de uma só frequência, propagando-se com uma velocidade de no ar, de massa específica homogênea . A escala do eixo vertical do gráfico representado na figura abaixo é definida por . Se, nas vizinhanças do monitor de pressão, a função deslocamento da onda é dada por .

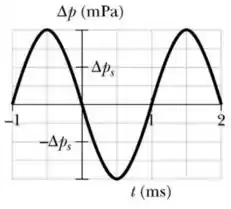
a) Determine a amplitude de pressão, , o período e o número de onda.

b) Obtenha e escreva a função que descreve o deslocamento .

c) Coloca-se um tubo com apenas uma extremidade aberta no caminho da onda sonora. Calcule qual deve ser o menor comprimento do tubo para que a onda estacionária formada em seu interior entre em ressonância.

d) Faça o desenho da onda estacionária de pressão no tubo, na situação do item c, indicando as extremidades aberta e a fechada.

e) Suponha, agora, que o monitor de pressão se encontre a uma distância da fonte sonora isotrópica (emite igualmente em todas as direções). Observa-se que a amplitude da onda de pressão é duplicada ao aproximarmos o monitor de em direção à fonte. De quanto aumenta a intensidade da onda sonora? Calcule a distância .

Um instrumento de sopro antigo e exótico em formato de um tubo lhe é dado de presente e ao tocá-lo você é capaz de produzir frequências sucessivas de ressonância a , e . A frequência do modo fundamental desse instrumento e a natureza do seu tubo são:

(a) , uma extremidade é aberta e a outra é fechada.

(b) e ambas as extremidades do tubo são abertas.

(c) , uma extremidade é aberta e a outra é fechada.

(d) , uma extremidade é aberta e a outra é fechada.

(e) e ambas as extremidades do tubo são abertas.

Um tubo, aberto em uma extremidade e fechado na outra, apresenta uma ressonância em , sendo esta a frequência mais baixa na qual o tubo oscila. Modos superiores de vibração vão ocorrer nas seguintes frequências:

(a) 1500 Hz e 2500 Hz

(b) 1000Hz e 2000 Hz

(c) 250 Hz e 125 hz

(d) 750 Hz e 1000 Hz

(e) 1000 Hz e 1500 Hz

Um tubo aberto pelas duas extremidades pode gerar ondas estacionárias de freqüências e , mas nenhuma onda estacionária pode ser gerada para freqüências entre essas duas. Pode-se dizer que:

(a) não correspondem, respetivamente, com as freqüências de vibração do primeiro e segundo harmônicos da onda estacionária.

(b) correspondem, respetivamente, as freqüências de vibração do primeiro e segundo harmônicos da onda estacionária.

(c) corresponde à freqüência do primeiro harmônico da onda estacionária, mas não é a freqüência do segundo harmônico.

(d) não é a freqüência de vibração do primeiro harmônico da onda estacionária, e corresponde à frequência associada ao segundo harmônico.

(e) correspondem, respetivamente, as freqüências do segundo e terceiro harmônicos da onda estacionária.

O que distingue uma mesma nota tocada com a mesma intensidade por um violino e por um piano?

1. Timbre.
2. Período.
3. Frequência fundamental.
4. Amplitude.
5. Velocidade.

Sobre os modos normais de vibração do ar no interior de um tubo, assinale a alternativa correta.

(a) A amplitude da pressão é sempre máxima (ventre) em uma extremidade aberta.

(b) Se uma extremidade é aberta e outra é fechada, cada modo tem pontos de desloamento nulo (nós) e pontos de amplitude máxima (ventres) em mesma quantidade.

(c) Se ambas extremidades são abertas, cada modo tem mais pontos de deslocamento nulo (nós) que pontos de deslocamento máximo ou mínimo (ventres).

(d) Sua frequência não depende do comprimento do tubo.

(e) Quanto mais longo o tubo, maiores serão suas frequências.

Sobre os modos normais de vibração do ar no interior de um tubo, assinale a alternativa correta.

(a) A amplitude da pressão é sempre máxima (ventre) em uma extremidade aberta.

(b) Se uma extremidade é aberta e outra é fechada, cada modo tem mais pontos de deslocamento nulo (nós) do que pontos de amplitude máxima (ventres).

(c) Sua frequência não depende do comprimento do tubo.

(d) Quanto mais longo o tubo, maiores serão suas frequências.

(e) Se ambas as extremidades são abertas, cada modo tem menos pontos de deslocamento nulo (nós) que pontos de amplitude máxima (ventres).

Um músico emite sons utilizando dois tubos de órgão de comprimentos iguais a e . Cada um deles é aberto numa extremidade e fechado na outra. A velocidade do som é .

1. Qual a frequência mais baixa que pode ser gerada com os dois tubos disponíveis?
2. Qual a frequência mais baixa na qual os dois tubos entram em ressonância simultaneamente?

​​​​Considere um tubo de comprimento que é aberto em ambas as extremidades. Quais serão os comprimentos de onda dos três primeiros sons claros (notas sonoras) de menores frequências emitidos por este tubo? 

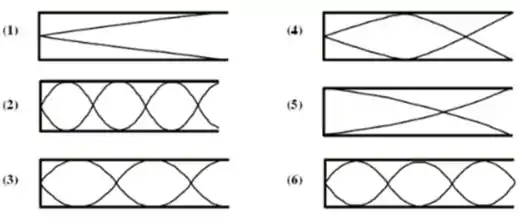
As figuras mostram ondas estacionárias em seis tubos de órgãos de mesmo comprimento. Cada tubo tem uma extremidade fechada e a outra aberta. Algumas das situações são impossíveis. Quais das figuras não mostram ondas estacionárias possíveis?

Um tubo cilíndrico, com uma extremidade aberta e outra fechada, tem um diâmetro e largura . Ele tem ar no seu interior. Suponha que a extremidade fechada do tubo esteja na posição . Considere a velocidade do som igual a .

1. Calcule a frequência natural de ressonância do tubo.
2. Para a frequência natural do tubo, considere que, na extremidade aberta do tubo, o deslocamento dos elementos de ar é máximo em e vale . Escreva a função para esse deslocamento no interior do tubo . Faça o gráfico dessa função em .

(Cap.16.4 – Ex. 24) A frequência fundamental de um tubo aberto em ambas as extremidades é . a) Qual é o comprimento desse tubo? Se agora fechamos uma extremidade, calcule b) o comprimento de onda e c) a nova frequência fundamental.

Se a velocidade do som é 340 m/s, as duas menores frequências de ressonância de um tubo de órgão com 0,5 m de comprimento, fechado em uma das extremidades, são aproximadamente:

a) 170 e 510 Hz;

b) 170 e 340 Hz;

c) 340 e 680 Hz;

d) 340 e 1020 Hz;

e) 57 e 170 Hz;

Dois tubos de um órgão de tubos possuem comprimentos de 85 cm e 80 cm, respectivamente. Ambos os tubos são abertos nas duas extremidades. Se ambos os tubos ressonarem em seus modos fundamentais, qual é o número de batimentos (máximos de intensidade sonora) por segundo que uma pessoa nas proximidades dos tubos ouviria?

(a) 12 Hz

(b) 12,5 Hz

(c) 5 Hz

(d) 24 Hz

(e) 25 Hz

. Considere um tubo aberto de altura onde há uma onda sonora vibrando no modo fundamental. Se de alguma maneira aumentarmos , podemos afirmar que:

A frequência de oscilação diminui e o número de onda diminui.

O comprimento de onda aumenta e a velocidade da onda dentro da onda diminui.

O número de onda aumenta e o comprimento de onda aumenta.

A velocidade é a mesma e comprimento de onda é o mesmo.

A frequência aumenta e o comprimento de onda aumenta.

Um tubo aberto nos dois lados produz uma onda sonora com frequência fundamental de . Se você fechar um dos lados a frequência fundamental, em Hz, será:

1. 43,75
2. 87,5
3. 350
4. 175
5. 700

Um tubo de órgão com uma extremidade aberta e a outra fechada é excitado em uma de suas frequências de ressonância. As extremidades aberta e fechada são, respectivamente:

a) um nó de pressão e um nó de deslocamento;

b) um nó de pressão e um nó de pressão;

c) um antinó de deslocamento e um nó de pressão;

d) um nó de deslocamento e um nó de deslocamento;

e) um antinó de pressão e um antinó de pressão;

Analise as afirmações abaixo:

(I) Em um tubo aberto nas duas extremidades, a frequência do terceiro harmônico é três vezes a frequência do primeiro harmônico.

(II) Em um tubo aberto em uma das extremidades e fechado na outra, os harmônicos pares não são excitados.

(III)Ondas estacionárias resultam da superposição de duas ondas que possuem mesma amplitude, frequência e sentido de propagação.

(IV)Quando a corda de um violão está vibrando em seu modo fundamental, o comprimento de onda do som produzido no ar é tipicamente o mesmo comprimento de onda da onda estacionaria na corda

(V)Uma corda pende verticalmente do teto. Um pulso é enviado corda acima. À medida que o pulso se aproxima do teto ele passa a viajar mais rapidamente.

a)Somente IV é falsa.

b)Somente I e II e V são verdadeiras

c)As afirmações IV e V são falsas.

d)Somente I, II e IV são verdadeiras.

e)As afirmações IV e V são verdadeiras.

3 - Os comprimentos de onda correspondentes aos harmônicos de um tubo de órgão que está aberto em uma extremidade e fechado na outra podem ser encontrados dizendo que o comprimento do tubo deve ser igual a

1. um número ímpar de múltiplos de um quarto de comprimentos de onda
2. um número ímpar de múltiplos de um terço de comprimentos de onda
3. um número ímpar de meios comprimentos de onda
4. um número inteiro de meios comprimentos de onda
5. um número inteiro de comprimentos de onda

O ouvido humano pode perceber sons na faixa de frequência . A figura mostra um alto-falante capaz de reproduzir todas as frequências nesta faixa. Coloca-se nas proximidades de um tubo sonoro com comprimento e aberto em ambas as extremidades. Determine o número total de frequências que vai produzir ondas estacionárias neste tubo.

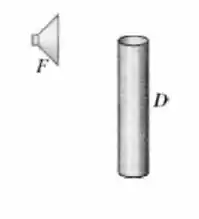
Dado: velocidade do som .

Considere dois tubos de mesmo comprimento, um aberto em ambas as extremidades, e o outro, fechado em uma extremidade. Seja o comprimento de onda do primeiro modo normal de vibração do ar no tubo aberto e o comprimento de onda do primeiro modo normal de vibração do ar no tubo com uma extremidade fechada. Considere as afirmações:

4. A pressão é constante nos extremos do tubo aberto e o deslocamento das moléculas de ar, portanto, é nulo.
5. A pressão é constante nos extremos do tubo aberto e o deslocamento das moléculas de ar, portanto, é máximo.

Qual(is) das afirmações acima é(são) verdadeira(s)?

(a) I.

(b) II.

(c) III.

(d) I e IV.

(e) I e V.

(f) II e IV.

(g) II e V.

(h) III e V.

Um tubo é cortado em duas partes. Numa das partes, com uma extremidade aberta e outra fechada, a frequência sonora fundamental é de 256 Hz. Na outra parte, com ambas as extremidades abertas, a frequência sonora fundamental é de 440 Hz. A velocidade do som no ar é 343 m/s. Qual é o comprimento original do tubo?

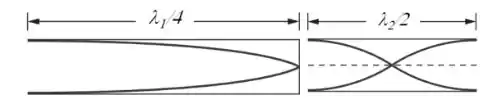
Considere um tubo de comprimento L fechado na sua extremidade esquerda e aberto para a atmosfera na sua extremidade direita, contendo ar em seu interior. Considere que a velocidade do som no ar seja dada por .

(a) Faça um desenho do tubo e represente os perfis das ondas geradas no seu interior, indicando as posições dos nós () e dos antinós () para os dois modos de frequência mais baixa das vibrações.

(b) Determine as frequências e dos dois modos mencionados na letra (a), escrevendo seus resultados em termos de e .

(c) Admitindo que e supondo que seja a frequência mais baixa que o ar no tubo entra em ressonância com o som emitido por um alto-falante próximo, determine o valor de .

(as respostas para este item devem ser dadas com casas decimais e em notação científica) Um tubo sonoro com duas extremidades abertas de comprimento que ressoa no modo (A velocidade do som no ar está dada na capa da prova).

1. Faça um desenho no tubo abaixo representando a onda sonora se propagando no tubo com duas extremidades abertas para . Identifique a posição e escreva os valores dos nós e dos anti-nós tomando por referência a extremidade esquerda como posição e a extremidade direita como posição



2. Determine a frequência emitida pelo tubo
3. Determine o comprimento de onda da onda emitida pelo tubo
4. Um segundo tubo com um tamanho ligeiramente menor que o primeiro também com a extremidade aberta é colocado próximo ao tubo descrito anteriormente. Quando passa ar por estes dois tubos, é ouvido um batimento com frequência de . Qual o comprimento deste segundo tubo

A figura mostra uma “‘flauta” simplificada, com a extremidade aberta. Há também uma grande abertura em ( próxima ao bocal) e dois orifícios em e , tais que e . Sabe-se que e que a velocidade do som é Qual a frequência que se espera ouvir ao soprar a flauta com o dedo tapando ?

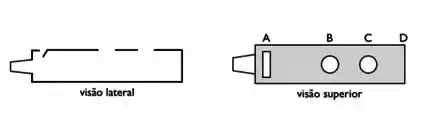
2. Não há como excitar uma onda no tubo, já que e estão à mesma pressão externa.
3. .
4. .
5. .

As frequências dos três primeiros harmônicos do som produzido por um tubo de órgão são 200, 600 e 1.000 Hz. Sendo a velocidade do som 340 m/s, o que se pode concluir a respeito do tubo?

a) o tubo é fechado em uma das extremidades e tem 0,425 m de comprimento;

b) o tubo é fechado em uma das extremidades e tem 0,95 m de comprimento;

c) o tubo é aberto nas duas extremidades e tem 0,95 m de comprimento;

d) o tubo é aberto nas duas extremidades e tem 0,475 m de comprimento;

e) nenhum tubo produz esse conjunto de harmônicos;

Duas frequências de ressonância sucessivas de um tubo são 1250Hz e 1750Hz. Desprezando efeitos de borda, determine:

a) O tubo está aberto nas duas extremidades ou em apenas uma? Justifique. (A resposta sem justificativa não será considerada)

b) O comprimento do tubo

c) Para o harmônico de , esboce as curvas da pressão em função da posição ao longo do tubo. Considere o tubo aberto em e indique claramente a posição dos nós.

d) Determine a frequência do modo fundamental.

e) Para o modo fundamental, esboce as curvas do deslocamento como função de Considere o tubo aberto em e indique claramente a posição dos nós.

f) Ainda para o modo fundamental, escreva a função de onda para o deslocamento considerando que a amplitude do deslocamento é . Considere o tubo aberto em .

Um tubo cilíndrico e de seção reta uniforme, tem suas extremidades abertas e em contato com o ar. Uma onda sonora no seu interior apresenta modos normais de vibração de frequências , onde . Ao fecharmos uma de suas extremidades com uma parede fixa, seus modos normais passam a ter frequências , onde . Qual a razão entre as frequências do n-ésimo modo normal de vibração nas duas situações, ? Quando esta razão se aproxima de 1?

(a) . Para frequências suficientemente baixas.

(b) . Para frequências suficientemente altas.

(c) . Para frequências suficientemente baixas.

(d) . Para frequências suficientemente altas.

(e) . Para nenhuma frequência.