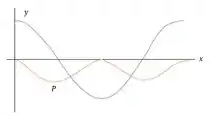
a)Faça um desenho de dado pela Equação (15.7) em função de x no instante t (digamos para t=0). Sobre os mesmos eixos, fala um desenho d potencia instantânea dado pela Equação (15.23). b) Explique a conexão entre o valor de e a inclinação da curva em função de x. Em particular, explique o que ocorre no ponto P=0, no qual não exite nenhuma transferência de energia instantânea. c) A grandeza sempre possui valor positivo. O que isso implica sobre o sentido da transferência de energia? d) Considere uma onda se propagando no sentido -x, para a qual . Calcule para esta onda e faça um gráfico de e em função de x no instante t (digamos para t=0). Que modificações ocorrem quando o sentido de propagação da onda se inverte?
Passo 1
Na parte (a) vamos desenhar os gráficos especificados.
Quando é o máximo, a inclinação é zero. A inclinação tem magnitude máxima quando .
Passo 2
-
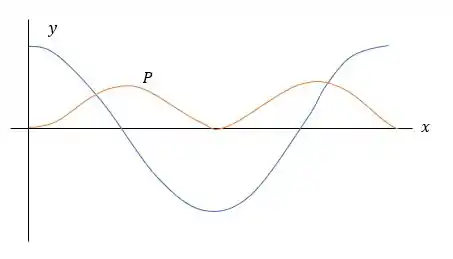
Passo 3
- A potência é máxima quando o deslocamento é zero e a potência é mínima quando a
- O fluxo de energia está sempre na mesma direção.
- Nesse caso, e a equação torna-se . A potência agora é negativa (a energia flui na direção ), mas as relações qualitativas da parte (b) permanecem inalteradas. O gráfico é esboçado a seguir:
magnitude do deslocamento é máxima.
Passo 4
Passo 5
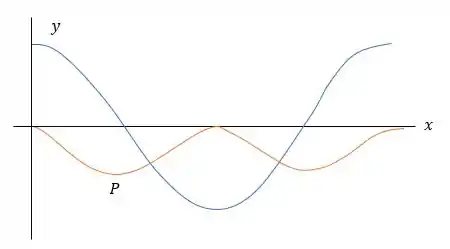
e estão fora de fase, portanto, para fixo, máximo corresponde a zero e corresponde a máximo.
Resposta
-
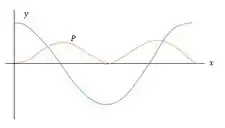
- Explicado no passo 3;
- Mesma direção;