Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 15.Problemas - Ex. 68

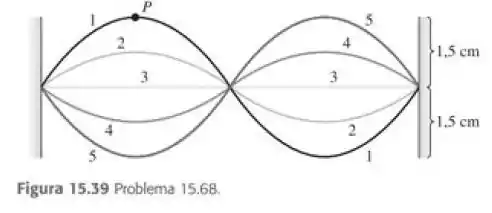
Uma corda de 50,0 cm de comprimento vibrando está sob uma tensão de 1,0 N. Os resultados de cinco fotografias estroboscopias sucessivas são mostradas na Figura 15.39. A taxa do estroboscópio é fixada em 5000 flashes por minuto, e observações revelam que o deslocamento máximo ocorreu nos flashes 1 e 5, sem nenhum outro máximo no intervalo entre eles. a) Calcule o periodo, a frequência e o comprimento de onda para as ondas progressivas nessa corda. b) Em que modo normal (harmônico) a corda esta vibrando? c) Qual é a velocidade das ondas progressivas na corda? d) Com que velocidade o ponto P se move quando a corda está na (i) posição 1 e (ii) posição 3? e) Qual é a massa dessa corda? (Seção 15.3).

Passo 1

O tempo entre as posições 1 e 5 é igual a T / 2 .

v   =   f λ .  

A velocidade dos pontos na corda é dada pelaequação:

v y x , t = ∂ y ( x , t ) ∂ t = ω A   s e n   ( k x - ω t )

Quatro flashes ocorrem da posição 1 à posição 5, portanto o tempo decorrido é 4 60 s 5000 = 0,048 s .

A figura no problema mostra que λ   =   L   =   0,500   m . No ponto P , a amplitude da onda estacionária é de   1,5   c m .

Passo 2

  1. Calculando o periodo, a frequência e o comprimento de onda para as ondas progressivas nessa corda, temos que:

    2. T 2 = 0,048 s e T = 0,096 s

    Agora que temos T , podemos calcular f :

    f = 1 T = 10,4   H z

    E

    λ = 0,500   m

    Passo 3

  2. A onda estacionária fundamental possui nós em cada extremidade e nenhum nó no meio. Essa onda parada tem um nó adicional. Este é o 1º harmônico e o 2º harmônico.

    3. Passo 4

  3. E a velocidade das ondas progressivas na corda é de:

    4. v = f λ = 10,4   H z 0,500   m = 5,20   m / s

    Passo 5

  4. Na posição 1, o ponto P está em seu deslocamento máximo e sua velocidade é zero. Na posição 3, o ponto P está passando através de sua posição de equilíbrio e sua velocidade é

    5. v m á x = ω A = 2 π f A = 2 π 10,4   H z 0,015 m = 0,980 m / s

    Passo 6

  5. E para calcularmos a massa da corda, fazemos:

v = F μ = F L m

que implica que

m = F L v 2 = ( 1,00 N ) ( 0,500 m ) 5,20 m s 2 = 18,5   g

A onda estacionária é produzida pelas ondas que se deslocam em direções opostas. Cada ponto da corda se move em SHM, e a amplitude desse movimento varia com a posição ao longo da corda.

Resposta

  1. T = 0,096 s ; f = 10,4   H z ;   λ = 0,500   m .  
  2. 1º harmônico e o 2º harmônico
  3. 5,20   m / s
  4. 0,980 m / s
  5. m = 18,5   g
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mede-se a velocidade v de propagação de ondas transversais num fio com uma extremidade presa a uma parede, que é mantido esticado pelo peso de um bloco suspenso da outra extremidade através de uma pol
A corda mi de um violino tem uma densidade linear de 0,5g / m e está sujeita a uma tensão de 80N , afinada para uma frequência ν = 660H z . (a) Qual é o comprimento da corda? (b) Para tocar a nota lá
(a) Mostre, diferenciando a expressão para a velocidade de propagação de ondas numa corda, que a variação percentual de velocidade Δ v / v produzida por uma variação Δ T / T da tensão na corda é dada
Três fios, cada um com comprimento L , são ligados em série por meio de suas extremidades formando um fio de comprimento igual a 3 L . As densidades lineares dos três fios são, respectivamente, μ 1 ,μ
Uma viga irregular de 1 75 0 N está pendurada horizontalmente por suas extremidades em um teto por dois fios verticais (A e B), cada um com 1,25 m de comprimento e pesando 2,5 N . O centro de gravidad