Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 18.1 - Ex. 74
Uma amostra de 2 mol de um gás monoatômico ideal tem uma pressão inicial de 2 atm e um volume inicial de 2 L. O gás é, então, conduzido através do seguinte ciclo quase estático: Ele se expande isotermicamente até que seu volume seja de 4L. Depois, ele é aquecido a volume constante até que sua pressão seja de 2 atm. A seguir, ele é resfriado à pressão constante de volta ao seu estado inicial.
- Mostre este ciclo em um diagrama PV;
- Determine a temperatura no final de cada etapa do ciclo;
- Calcule o calor absorvido e o trabalho realizado pelo gás durante cada etapa do ciclo.
Passo 1
Obs: uma observação antes de começar. O enunciado dessa questão está com um probleminha de tradução. Faltou ele dizer que temos 2 mols do gás, beleza? Aí na resolução, vamos considerar esse valor.
a) Muito bem, nós precisamos construir um diagrama PV para os três processos descritos. Vamos analisar separadamente cada um:
Processo 1-2) Nós temos a pressão inicial de e um volume inicial de . Neste passo o gás se expande isotermicamente (temperatura constante) até que seu volume final seja .
Precisamos saber também a pressão final , para saber o ponto final desse processo no diagrama PV. Mas como achamos?
Vamos começar usando a lei dos gases:
Como a temperatura é constante, , então
Isolando a pressão:
Substituímos:
Esse processo no diagrama fica sendo então uma curva com concavidade para cima que liga o ponto ao .
Processo 2-3) O gás é aquecido a volume constante, então , até que sua pressão seja de 2 atm. Aqui já temos todas as informações! Como o volume é constante, vamos sair do ponto e subir reto ao ponto
Processo 3-1) Aqui ele volta ao seu estado inicial a pressão constante, então vamos fazer um segmento de reta horizontal ligando a .
Sabemos tudo o que precisamos. Agora vamos para o diagrama PV:
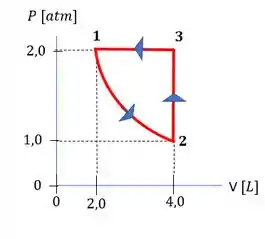
Passo 2
b) Neste passo vamos focar em achar as temperaturas pedidas na letra b. Vamos!
Processo 1-2) Temos aqui a expansão isotérmica, ou seja, a temperatura é igual ao longo deste caminho. Então podemos usar
Para achar a temperatura no início do processo, e como ela é constante, também vai ser a temperatura no fim.
Isolamos T:
Temos que passar a pressão para para usar a fórmula
E o volume para :
Lembrando que temos e que podemos substituir os valores:
Como a temperatura final é a mesma:
Processo 2-3) O gás é aquecido até e . Então a temperatura final se dá no ponto 3. Usando a mesma equação da anterior:
Novamente precisamos passar a pressão para e o volume para .
Processo 3-1) A temperatura final neste passo será a do ponto 1, que é igual a
Passo 3
Calma, guerreiros! Estamos finalizando. Só precisamos do calor absorvido e o trabalho realizado pelo gás durante cada etapa do ciclo.
Vamos lá?
Processo 1-2) Aqui temos uma expansão isotérmica, ou seja, o gás não sofreu alteração na temperatura. Quando não há mudança de temperatura, podemos assumir que:
Se usarmos a primeira lei da termodinâmica a partir daí:
Mas queremos o trabalho realizado pelo gás e não o trabalho sobre o gás. Mas relaxa, a gente pode relacionar esses dois tipos de trabalho assim:
Substituindo a primeira lei
Em uma expansão isotérmica o trabalho pode ser definido como:
Substituindo:
Assim:
Processo 2-3) O gás é aquecido a volume constante, se o volume não muda quer dizer que não houve trabalho, então
Então o calor também zera? Não. Neste caso, o gás não realizou trabalho, mas aumentou sua temperatura, ou seja, houve variação da energia interna. Segundo a primeira lei:
A variação da energia pode ser calculada como:
Neste caso, g são os graus de liberdade do gás. Para um gás monoatômico, :
Substituindo os valores:
Para finalizar!
Processo 3-1) Aqui temos um processo à pressão constante, então o trabalho pode ser calculado simplesmente por:
Como o volume diminuiu, o trabalho foi realizado sobre o gás. Por isso, nosso trabalho realizado pelo gás fica negativo. Lembrando de passar o volume para e a pressão para :
E para o calor podemos usar essa expressão para pressão constante:
Sendo que para um gás ideal monoatômico
Substituindo essa expressão na expressão logo acima:
E susbtituindo na expressão do calor
Substituímos os dados
Resposta
- |