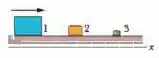
Amplificador de velocidade. Na Fig. 9-75, o bloco 1, de massa , desliza ao longo de um eixo em um piso sem atrito, com uma velocidade , até sofrer uma colisão elástica unidimensional com o bloco 2, de massa , inicialmente em repouso. Em seguida, o bloco 2 sofre uma colisão elástica unidimensional com o bloco 3 de massa , inicialmente em repouso. (a) Qual é a velocidade do bloco 3 após a colisão? (b)A velocidade, (c) a energia cinética e (d) o momento do bloco 3 são maiores, menores ou iguais aos valores iniciais do bloco 1?

O resultado do item anterior mostra que a velocidade do bloco 3 é maior que a velocidade inicial do bloco 1.

Bom pessoal , nós sabemos que a energia cinética do bloco 3 é dada por :

Vemos, portanto, que a energia cinética do bloco 3 é menor que a energia cinética inicial do bloco 1.

O momento do bloco 3 , por sua vez , pode ser obtido através da relação :

Portanto, o momento do bloco 3 é menor que o momento inicial do bloco 1.