Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.Problemas Adicionais - Ex. 104
Em um jogo de sinuca, a bola branca se choca com outra bola inicialmente em repouso. Após o choque, a bola branca se move com uma velocidade escalar de ao longo de uma reta que faz um ângulo de com a direção do movimento da bola branca antes do choque e a segunda bola tem urna velocidade escalar de . Determine (a) o ângulo entre a direção do movimento da segunda bola e a direção do movimento da bola branca antes do choque e (b) a velocidade escalar da bola branca antes do choque. (c) A energia cinética ( dos centros de massa, não considere as rotações) é conservada?
Passo 1
Então galera , bora dar uma olhada na ilustração do problema :
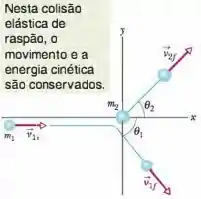
Chamamos a bola branca de bola 1 e a outra bola de bola 2. Aplicando a lei de conservação do momento às componentes e do momento total do sistema de duas bolas, temos que :
As massas são iguais e se cancelam nas equações. Explicitando na segunda equação, obtemos:
O ângulo entre a direção do movimento da segunda bola após o choque e a direção do movimento da bola branca antes do choque é, portanto, .
Passo 2
Bom pessoal , nós podemos usar a primeira equação para determinar a velocidade inicial da bola branca :
Passo 3
A energia cinética inicial , por sua vez , é dada por :
e a energia cinética final é :
Este resultado mostra que a energia cinética não é conservada.
Resposta
A energia cinética não é conservada.
Tranquilo galera? Bora resolver mais questões então