Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 23.Exercícios e Problemas - Ex. 6

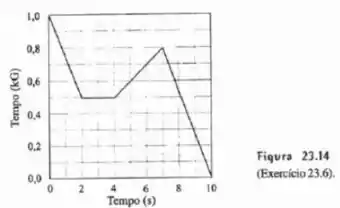
Um anel circular de raio valendo 5,0   c m está em uma região onde um campo magnético homogêneo, paralelo ao seu eixo, varia no tempo como mostra a Figura 23.14. Faça um gráfico de fem induzida no anel.

Passo 1

Antes de começar a resolver o problema, segue uma correção: o gráfico no livro diz que o eixo y representa um tempo (???) em kilogauss, quando na verdade ele se referia ao campo magnético. Portanto, interprete o gráfico como sendo o gráfico do campo em função do tempo.

Outra observação importante, 1   G = 10 - 4   T , logo

1   k G = 0,1   T

Feita essa discussão, podemos partir para o problema...

O primeiro passo é escrever o fluxo magnético no anel:

Φ B = B ⋅ A → ϕ B = π r 2 ⋅ B

Assim, pela lei de Faraday, a fem induzida será

E = - d Φ B d t = - π r 2 d B d t

De t = 0   s para t = 2   s , temos

d B d t = Δ B Δ t = - 0,05 2 = - 0,025   T / s

Já entre t = 2   s e t = 4   s o campo é constante, de modo que

d B d t = 0

No intervalo seguinte, entre t = 4   s e t = 7   s , temos que

d B d t = Δ B Δ t = 0,03 3 = 0,01   T / s

Por fim, para t > 7   s , achamos

d B d t = Δ B Δ t = - 0,08 3 = - 0,027   T / s

Daí, basta multiplicar por - π r 2 = - 3,14 ⋅ 5 ⋅ 10 - 2 2 = - 7,8 ⋅ 10 - 3   m 2 que achamos a fem induzida:

E = 1,96 ⋅ 10 - 4   V ,               t < 2   s 0   V ,                   2   s < t < 4   s - 0,78 ⋅ 10 - 4   V ,             4   s < t < 7   s 2,12 ⋅ 10 - 4   V ,             t > 7   s

Passo 2

A seguir fazemos o esboço do gráfico de E em função do tempo:

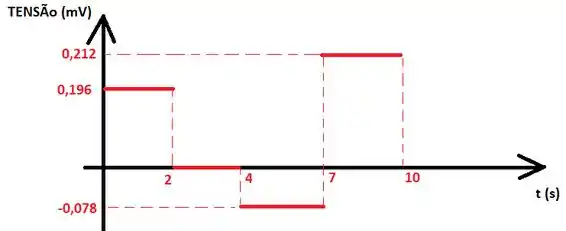
Resposta

Esboço de gráfico.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Qual é a frequência da radiação de microondas que tem comprimento de onda de 3.00c m ? (b) Usando a Tabela 30-1, estime a razão entre o menor comprimento de onda da luz verde e o menor comprimento
A cor predominante da luz do Sol está na região amarelo-verde do espectro visível. Estime o valor do comprimento de onda e da frequência da cor predominante emitida pelo nosso Sol. Dica: Veja a Tabela
Há uma corrente de 10A em um resistor que está conectado em série com um capacitor de placas paralelas. As placas do capacitor têm uma área de 0.50m 2 e não há nenhum dielétrico entre elas. (a) Qual é
Nos capacitores referidos neste problema há apenas espaço vazio entre as placas. (a) Mostre que um capacitor de placas paralelas tem uma corrente de deslocamento na região entre suas placas que é dada
Demonstre a validade da forma generalizada da lei de Ampère (Equação 30-4) mostrando que ela fornece o mesmo resultado que a lei de Biot-Savart (Equação 27 -3) em uma situação específica. A figura aba