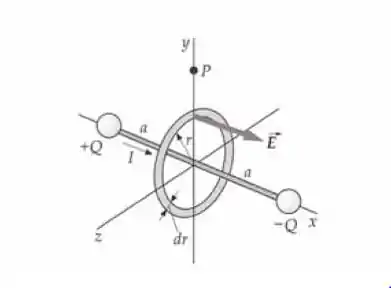
Demonstre a validade da forma generalizada da lei de Ampère (Equação 30-4) mostrando que ela fornece o mesmo resultado que a lei de Biot-Savart (Equação 27 -3) em uma situação específica. A figura abaixo mostra duas cargas puntiformes momentaneamente iguais, com sinais opostos (+Q e -Q) no eixo x em e , respectivamente. No mesmo instante, há uma corrente I no fio que as conecta, como mostrado. O ponto P está no eixo y em . (a) Use a lei de Biot-Savart para mostrar que a magnitude do campo magnético no ponto P é dada por . (b) Agora considere uma faixa circular de raio r e largura dr no plano cujo centro está na origem. Mostre que o fluxo do campo elétrico através desta faixa é dado por . (c) Use o resultado da parte (b) para mostrar que o fluxo elétrico total . (d) Encontre a corrente de deslocamento através de S, e mostre que . (e) Finalmente, mostre que a forma generalizada da Lei de Ampère (Equação 30-4) fornece o mesmo resultado que a magnitude encontrada na parte (a).

Primeiramente, expressaremos o a força do campo magnético em P usando a expressão para B devido a um segmento de fio reto:

Onde :

(1)

Agora, expressaremos o fluxo magnético através da faixa circular de raio r e largura dr no plano yz:

Devido ao dipolo o campo elétrico possui a seguinte representação:

Substituindo , obtemos:

Multiplicando ambos os lados por :

Agora, integrando de 0 até R, temos:

A corrente de deslocamento é definida por:

A corrente total é a soma de e :

Aplicando a equação 30-4 (a forma generalizada da lei de Ampère), obtemos:

Substituindo a corrente total, temos que:

AÍ ESTÁ, tudo feito com sucesso! É TUDO POR HOJE, bons estudos ;). Obs: Vai beber água que tá na hora, obrigado, de nada.