Enunciado
Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 2.Problemas - Ex. 1
O ângulo de incidência para o qual o raio refletido é perpendicular ao raio refratado chama-se ângulo de Brewster. (a) Obtenha o ângulo de Brewster em função do índice de refração relativo do meio 2 em relação ao meio 1; (b) Calcule para as seguintes interfaces: ar/água; ar/vidro comum.
Passo 1
Opa! Vamos lá!
Quando o ângulo refletido for perpendicular ao raio refratado, o ângulo de incidência se chama ângulo de Brewster, . Vamos desenhar essa situação;
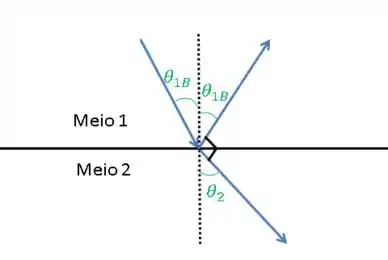
Já coloquei o ângulo de incidência igual ao ângulo refletido, pela de de reflexão.
Olhando pra figura, sabemos que o raio refletido e o refratadao são perpendiculares, então
Beleza! Guarde esse resultado aí.
Passo 2
Vamos aplicar a lei de Snell na interface entre os meios
Vamos substituir o que achamos lá no passo 1.
Pela regra de soma de arcos, temos
Show!! Então a lei de snell fica:
Ou seja,
Onde, é o índice de refração relativo do meio 2 em relação ao meio 1.
Passo 3
b)
Para a interface ar-água. Temos então e
Para a interface ar-vidro, temos: e .
Resposta
A)Demosntração
b)