Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 1.1 - Ex. 14
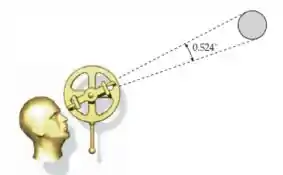
O ângulo subtendido pelo diâmetro da lua em um ponto na Terra é cerca de (veja a figura). Use essa informação e o fato de que a lua está a cerca de de distância para encontrar o diâmetro da Lua. Dica: o ângulo pode ser determinado a partir do diâmetro da lua e da distância até a lua.
Passo 1
Falaa! A gente quer o diâmetro da lua. Ele nos dá a distância entre a lua e um ponto da terra e também nos dá o ângulo subtendido pelo diâmetro da lua, que é esse ângulo mostrado na figura do enunciado.
Para começar, vamos lembrar de uma fórmula bastante importante da geometria plana. Se a gente tiver um setor circular caracterizado por um ângulo , assim:
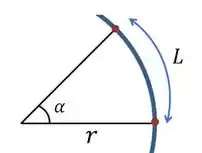
Podemos achar esse comprimento , usando
Sendo que é o raio do círculo onde esse setor circular está contido. É importante saber que, quando o ângulo é muito pequeno, o arco se aproxima bastante de um segmento de reta, porque ele vai ser bem pequeno também.
Então essa situação do setor circular ficaria mais ou menos assim:
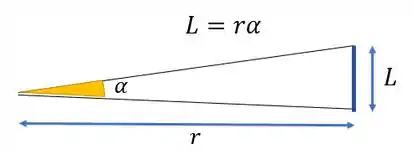
Como nessa questão estamos tratando de um ângulo de apenas , um ângulo bem pequeno, nós podemos tratar o diâmetro da lua (que é um segmento de reta) como se fosse um pequeno arco.
Passo 2
Nesse caso, a distância até a lua cumpriria o papel do raio do círculo imaginário, e então o diâmetro da Lua seria dado pela seguinte fórmula:
Aí vamos usar essa expressão para achar o nosso diâmetro. Só vamos ter cuidado com as unidades. A distância entre o ponto e a lua é
A distância foi dada em megametros , ou seja, . Então temos
Já o ângulo precisa ser convertido para radianos. Para sair de graus e ir para radianos, precisamos multiplicar nosso ângulo por :
Agora a gente substitui esses valores na nossa fórmulinha para o diâmetro:
Resposta
O diâmetro da Lua é aproximadamente .