Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 80
A extremidade superior do fio enrolado em redor do cilindro da figura está segura por uma mão que acelera para cima, de modo que o centro de massa do cilindro não se move, enquanto o cilindro gira. Determine (a) a tensão no fio, (b) a aceleração angular do cilindro e (c) a aceleração da mão.
Passo 1
Bora lá, galera, vamos analisar o movimento de um cilindro, à medida que puxamos um fio que está enrolado em volta dele. A situação, fisicamente, vai ter essa cara aqui:
Passo 2
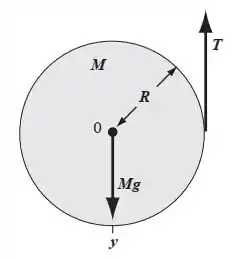
- Ele falou assim no enunciado: “o centro de massa do cilindro não se move, enquanto o cilindro gira”. Então, o cilindro está fixo ali no centro dele, e só vai ter rotação. Como está parado na vertical, podemos dizer que ele está em equilíbrio nessa direção.
- A segunda lei de Newton para a rotação vai nos dar:
- Nós podemos relacionar a aceleração tangencial e angular pela equação .
Passo 3
Agora vamos substituir o que já conhecemos:
Passo 4
Resposta
Exercícios de Livros Relacionados
Um carro de 1200k g está sendo retirado da água por um guincho. No momento em que o carro está 5,0 m acima da água, a caixa de engrenagens quebra e o tambor do guincho gira livremente enquanto o carro
Uma esfera maciça e unifome de massa M e raio R está livre para girar em torno de um eixo horizontal que passa pelo seu centro. Um cortão está enrolado em torno da esfera e preso a um objeto de massa
Dois corpos estão preso a cordas que, por sua vez, estão presas a duas rodas que giram em torno do mesmo eixo, como mostrado na figura. As uas rodas estão soldadas, e modo a formarem um único objeto r
Dois corpos, de massas m 1 = 500 g e m 2 = 510 g , estão ligados por um fio de massa desprezível que passa por uma polia sem atrito. A polia é um isco uniforme de 50,0 g com um raio de 4,00 c m . O fi