Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 80

Em seu aniversário, você foi presenteado com uma polia. Trata-se de uma polia realmente grande, com 12 cm de diâmetro e massa de 2,0 kg. Você está preocupado em saber se a polia é homogênea, ou seja, se sua massa está igualmente distribuída ou está mais concentrada próximo ao eixo ou à borda. Para descobrir, você pendura a polia em um gancho, enrola várias voltas de barbante em torno dela e suspende nela seu livro de física de 1,0 kg a 1,0 m acima do piso. Com um cronômetro, você constata que decorrem 0,71 s para que o livro atinja o piso. O que você pode concluir a respeito da polia?

Passo 1

A polia é um corpo rotativo rígido.

Vamos visualizar a situação:

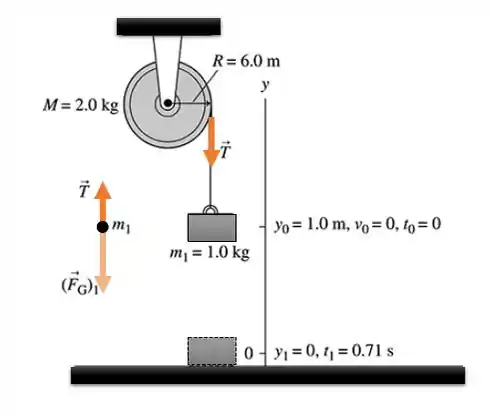
Colocamos a origem do sistema de coordenadas no chão. A polia gira em torno de seu centro.

Passo 2

Usando a cinemática para o livro de física ( m a s s a = m 1 ),

y 1 = y 0 + v 0 t 1 - t 0 + 1 2 a t 1 - t 0 2

Substituindo por números, temos:

0 m = 1   m + 0   m + 1 2 a 0,71 s - 0 s 2

⇒ a = - 3,967   m / s 2

Passo 3

Como o torque que atua na polia é

τ = - T R = I α ,

nós temos

I = - T R α = - T R a / R = - T R 2 a

Podemos comparar o valor medido de I para a polia com o valor teórico. Primeiro precisamos encontrar a tensão T . No diagrama do corpo livre, a segunda lei do movimento de Newton é:

T - m 1 g = m 1 a .

Isso significa:

T = m 1 g + a = ( 1   k g ) ( 9,8   m / s 2 - 3,967   m / s 2 ) = 5,833   N

Passo 4

Com esses valores de T e a , agora podemos encontrar   I como:

I = - T R 2 a = - 5,833   N ⋅ 0,06 m 2 ( - 3,967   m / s 2 ) = 5,3 × 10 - 3 k g ⋅ m 2

Passo 5

Vamos agora calcular os valores teóricos de I :

Aro sobre o centro: I = M R 2 = 2 k g ⋅ 0,06 m 2 = 7,2 × 10 - 3   k g ⋅ m 2

Disco sobre o centro: I d i s c o = 1 2 M R 2 = 1 2 2   k g 0,06 m 2 = 3,6 × 10 - 3   k g ⋅ m 2

Resposta

Desde que I d i s c o < I < I a r o , a massa do disco não é distribuída uniformemente. A massa é concentrada perto da borda.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um disco de 5,0 kg e 60 cm de diâmetro gira em torno de um eixo que passa pela borda do disco. O eixo é paralelo ao piso.O disco é mantido com seu centro de massa na altura do eixo e, depois, é libera
Suponha que o túnel de conexão do Exemplo 12.11 tenha uma massa de 50.000 kg.a. A que distância do foguete de 100.000 kg se encontra o centro de massa da estrutura inteira?b. Qual é a velocidade angul
Um aro de massa M e raio R gira em torno de um eixo que passa pela borda do aro. Partindo de sua posição mais alta, é dado um pequeno empurrão no disco a fim de pô-lo em rotação. Na posição mais baixa
Os blocos de massas m 1 e m 2 estão ligados por um barbante de massa desprezível que passa por uma polia, como mostrado na FIGURA P12.71. A polia gira praticamente sem atrito sobre pequenas esferas. A