Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 76

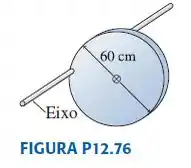
Um disco de 5,0 kg e 60 cm de diâmetro gira em torno de um eixo que passa pela borda do disco. O eixo é paralelo ao piso.

O disco é mantido com seu centro de massa na altura do eixo e, depois, é liberado.

a. Qual é a aceleração angular inicial do cilindro?

b. Qual é a velocidade angular do cilindro quando ele estiver diretamente abaixo do eixo?

Passo 1

O disco é um corpo rígido girando em um eixo que passa por uma borda. A energia potencial gravitacional é transformada em energia cinética rotacional quando o disco é liberado.

Vamos visualizar:

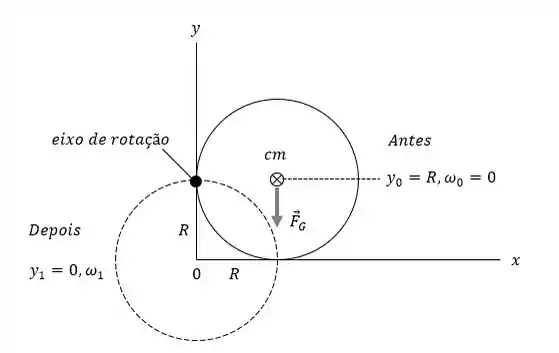
Colocamos a origem do sistema de coordenadas a uma distância R logo abaixo do eixo. Na posição inicial, o centro de massa do disco está no mesmo nível do eixo. O centro de massa do disco na posição final é coincidente com a origem do sistema de coordenadas.

Passo 2

  1. O torque é devido à força gravitacional no disco atuando no centro de massa. Portanto

    2. τ = m g R = ( 5   k g ) ( 9,8   m / s 2 ) ( 0,30   m ) = 14,7   N ⋅ m

    O momento de inércia sobre a borda do disco é obtido usando o teorema do eixo paralelo:

    I = I c m + m R 2 = 1 2 m R 2 + m R 2 = 3 2 m R 2

    Substituindo valores:

    I = 3 2 5   k g 0,30   m 2 = 0,675   k g ⋅ m 2

    Passo 3

    Agora que temos τ e I , podemos calcular α :

    α = τ I = 14,7   N ⋅ m 0,675   k g ⋅ m 2 = 22   r a d / s 2

    Passo 4

  2. A equação de conservação de energia K f + U g f = K i = U g t é:

1 2 I ω 1 2 + m g y 1 = 1 2 I ω 0 2 + m g y 0

⇒ 1 2 I ω 1 2 + 0   J = 0   J + m g R

ω 1 = 2 m g R I = 2 ( 5   k g ) ( 9,8   m / s 2 ) ( 0,30 m ) 0,675   k g ⋅ m 2 = 6,6   r a d / s

Uma velocidade angular de 6,6   r a d / s (ou   1,05   r o t a ç õ e s / s ) à medida que o centro de massa do disco atinge abaixo do eixo é razoável.

Resposta

α = 22   r a d / s 2

ω 1 = 6,6   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Três partículas de 0,50k g formam um triângulo equilátero de 0,60m de lado. As partículas estão ligadas por barras de massa desprezível. Qual é o momento de inércia desse corpo rígido em relação (a) a
Uma boladeira é composta por três esferas pesadas iguais, ligadas a um ponto comum por cordas resistentes de mesmo comprimento (figura a). Para lançar esta arma inventada na América do Sul você segura
Um objeto deve estar em rotação para possuir momento de inércia?Explique
Um disco fino de 100g de massa e 8,0c m de diâmetro gira em torno de um eixo que passa por seu centro com 0,15J de energia cinética. Qual é o módulo da velocidade de um ponto da borda do disco?
Qual é a energia cinética de rotação da Terra? Considere que a Terra seja uma esfera homogênea. Os dados para a Terra podem ser encontrados na parte interna da contracapa deste livro.