Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 71

Os blocos de massas m 1 e m 2 estão ligados por um barbante de massa desprezível que passa por uma polia, como mostrado na FIGURA P12.71. A polia gira praticamente sem atrito sobre pequenas esferas. A massa m 1 desliza sobre uma superfície horizontal livre de atrito. A massa m 2 é liberada a partir do repouso.

a. Considere que a massa da polia seja desprezível. Determine a aceleração de m1 e a tensão no barbante. Este é um problema de revisão do Capítulo 7.

b. Suponha que a polia tenha massa m p e raio R. Determine a aceleração de m 1 e a tensão nas partes superior e inferior do barbante. Verifique se suas respostas concordam com o item a para o caso de m p = 0 .

Passo 1

Galera, suponha que a corda não escorregue na polia.

Vamos desenhar o diagrama de corpo livre.

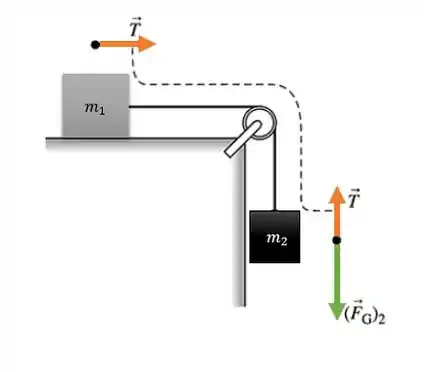
Os diagramas de corpo livre para os dois blocos e a polia são mostrados. A tensão na corda exerce uma força ascendente no bloco m 2 , mas uma força descendente na borda externa da polia. Da mesma forma, a corda exerce uma força no bloco m 1 para a direita, mas uma força para a esquerda na borda externa da polia.

Observe:

Passo 2

  1. Aplicando a segunda lei de Newton para m 1 e m 2 é, respectivamente:

    2. T = m 1 a 1 e T - m 2 g = m 2 a 2 .

    Usando a restrição:

    - a 2 = + a 1 = a ,

    Nós temos que:

    T = m 1 a e - T + m 2 g = m 2 a .

    Adicionando essas equações, nós ficamos com:

    m 2 g = m 1 + m 2 a ,

    ou

    a = m 2 g m 1 + m 2

    ⇒ T = m 1 a = m 1 m 2 g m 1 + m 2 .

    Passo 3

  2. Quando a polia tem massa m, as tensões ( T 1 e T 2 ) nas partes superior e inferior da corda são diferentes. A segunda lei de Newton para m 1 e a polia são:

T 1 = m 1 a e T 1 R - T 2 R = - I α

Estamos usando o sinal de menos com α porque a polia acelera no sentido horário. Além disso, a   =   R α . Assim, T 1 = m 1 a e:

T 2 - T 1 = I R a R = a I R 2

A adição dessas duas equações fornece

T 2 = a m 1 + I R 2

Passo 3

A segunda Lei de Newton para m 2 é:

T 2 - m 2 g = m 2 a 2 = - m 2 a 2 = - m 2 a .

Usando a expressão acima para T 2 :

a m 1 + I R 2 + m 2 a = m 2 g

⇒ a = m 2 g m 1 + m 2 + 1 2 m p o l i a

Com esse valor para a , agora podemos encontrar T 1 e T 2 :

T 1 = m 1 a = m 1 m 2 g m 1 + m 2 + 1 2 m p o l i a

T 2 = a m 1 + I R 2 = m 2 g m 1 + m 2 + 1 2 m p o l i a m 1 + 1 2 m p o l i a = m 2 m 1 + 1 2 m p o l i a m 1 + m 2 + 1 2 m p o l i a .

Passo 4

Para m = 0   k g , as equações para a , T 1 , e T 2 da parte (b) simplificam para:

a = m 2 g m 1 + m 2 e T 1 = m 1 m 2 g m 1 + m 2 e T 2 = m 1 m 2 g m 1 + m 2 .

Eles concordam com os resultados da parte (a).

Resposta

  1. a = m 2 g m 1 + m 2 e T = m 1 m 2 g m 1 + m 2
  2. a = m 2 g m 1 + m 2 + 1 2 m p o l i a , T 1 = m 1 m 2 g m 1 + m 2 + 1 2 m p o l i a e T 2 = m 2 m 1 + 1 2 m p o l i a m 1 + m 2 + 1 2 m p o l i a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esfera de massa M e raio R é rigidamente fixada a um bastão fino de raio r que passa por dentro dela, a uma distância R de seu centro. Um barbante é enrolado em torno do bastão e o puxa com uma te
Uma haste comprida e delgada, de massa M e comprimento L, está em pé sobre uma mesa. Sua extremidade inferior gira sobre um pivô livre de atrito. Um empurrão muito fraco faz a haste tombar. Ao colidir
As massas M e m estão ligadas por uma haste rígida, de massa desprezível e comprimento L. Elas giram em torno de um eixo perpendicular situado a uma distância x da massa M.a. Para rotação com velocida
O disco de 2,0 kg e 30 cm de diâmetro da FIGURA P12.72 gira a 300 rpm. Que valor de força de atrito deve o freio exercer na borda do disco a fim de pará-lo em 30 s?
Uma esfera oca está rolando sobre um piso horizontal a 5,0 m/s quando chega à base de uma rampa com 30 ° de inclinação. Que distância ela percorrerá rolando na rampa antes de inverter seu movimento?