Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 77

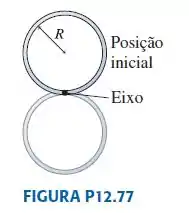
Um aro de massa M e raio R gira em torno de um eixo que passa pela borda do aro. Partindo de sua posição mais alta, é dado um pequeno empurrão no disco a fim de pô-lo em rotação. Na posição mais baixa, quanto vale (a) a velocidade angular e (b) a velocidade do ponto inferior do disco?

Passo 1

O bastidor é um corpo rígido que gira em torno de um eixo na borda do bastidor. O torque gravitacional no aro faz com que ele gire, transformando a energia potencial gravitacional do centro de massa do aro em energia cinética rotacional.

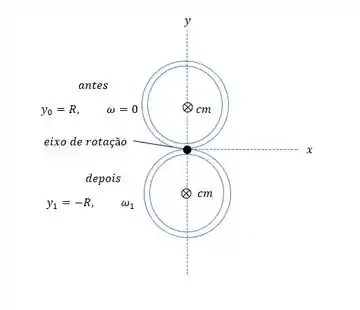
Colocamos a origem do sistema de coordenadas na borda do bastidor no eixo. Na posição inicial, o centro da massa é uma distância R acima da origem, mas é uma distância R abaixo da origem na posição final.

Passo 2

  1. Aplicando o teorema do eixo paralelo,

    2. I b o r d a = I c m + m R 2 = m R 2 + m R 2 = 2 m R 2 .

    Usando esta expressão na equação de conservação de energia K f + U g f = K i + U g i :

    1 2 I b o r d a ω 1 2 + m g y 1 = 1 2 I b o r d a ω 0 2 + m g y 0

    1 2 2 m R 2 ω 1 - m g R = 0   J + m g R

    ⇒ ω 1 = 2 g R

    Passo 3

  2. A velocidade do ponto mais baixo do aro é

v = ω 1 2 R = 2 g R 2 R = 8 g R .

Observe que a velocidade do ponto mais baixo do loop envolve uma distância de 2R em vez de R.

Resposta

  1. ω 1 = 2 g R
  2. v = 8 g R .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

84. || Uma bala de 10 g colide a 400 m/s com uma porta de 10 kg e 1,0m de largura, atingindo-a na borda do lado oposto ao das dobradiças.A bala se incrusta na porta, abrindo-a. Qual é a velocidadeangu
87. ||| Uma mesa giratória de 200 g e 40 cm de diâmetro gira sem atritoa 60 rpm sobre um rolamento de pequenas esferas. Um bloco de20 g está posicionado no centro da mesa giratória. Uma mola comprimid
85. || Uma esfera maciça de raio R é posicionada a uma altura de 30 cmsobre uma rampa com 15° de inclinação. Ela é liberada e rola, semdeslizar, até a base da rampa.a. De que altura deveria ser libera
2. Se a velocidade angular ω se mantiver constante, em que fator deve R variar a fim de dobrar a energia cinética de rotação do haltere da FIGURA Q12.2?
3. A FIGURA Q12.3 mostra três discos em rotação, todos de mesma massa. Ordene em seqüência decrescente as energias cinéticas de rotação de K a a K c .