Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 48
Ao fazer compras, você coloca diversas maçãs no dinamômetro do setor de frutas e legumes. O dinamômetro marca 20 N, e você usa sua régua (que sempre carrega consigo) para constatar que a bandeja desceu 9,0 cm quando as maçãs foram adicionadas. Se você bater no fundo da bandeja repleta de maçãs, fazendo com que ela balance um pouco, qual será a sua frequência de oscilação? Despreze a massa da bandeja
Passo 1
O prato da balança estará equilibrado por duas forças:
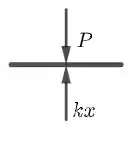
O peso das maças e a força elástica pela mola. O peso das maças vale e !
Passo 2
Pelo equilíbrio:
Passo 3
Sabemos que:
pois . Logo,
Resposta
A frequência é .
Exercícios de Livros Relacionados
A FIGURA Q14.5 mostra um gráfico velocidade versus tempo para uma partícula em MHS. a. Quanto vale a constante de fase ϕ 0 ? Explique. b. Qual é a fase da partícula em cada um dos três pontos, numerad
13.2E O movimento de um oscilador harmônico é descrito por x = 0,75cm. cos ( 5,0t/s ) - 0,40cm. sen 5,0t/s . Escreva este movimento na forma de x = x m cos ω t + ϕ .
13.11E Calcule o módulo dos números: z 1 = 4,0 + 3,0 i ,z 2 = 15 e i ϕ ,z 3 = 20 i cos 30 ° + sin 60 ° .
13.12E Coloque os números z 1 = 10 + 8,67 i , z 2 = 20 sin 240 ° + i cos 210 ° na representação de Euler.
13.13E Considere as n raízes enésima da unidade, ou seja, as n soluções de z = 1 n , para A) n = 2 , B) n = 3 e C) n = 4 . Para cada valor de n , represente as soluções encontradas em um gráfico no pl